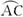题目内容
如图1-1-6,以梯形ABCD的对角线AC及腰AD为邻边作?ACED,DC的延长线交BE于F,求证:EF=BF.
图1-1-16
思路分析:在△EAB中,OF∥AB.要说明EF=BF,只要说明O是AE的中点,而O是平行四边形对角线的交点,根据平行四边形的对角线互相平分性质,可以知道O是AE的中点,于是问题得证.
证明:连结AE交DC于O,∵四边形ACED是平行四边形,
∴O是AE的中点(平行四边形对角线互相平分).
∵四边形ABCD是梯形,∴DC∥AB.
在△EAB中,OF∥AB,又O是AE的中点,
∴F是EB的中点.∴EF=BF.
深化升华 证题时,当一个条件有几个结论时,要选择与其有关联的结论.本题可延长EC,在梯形ABCD内构造平行四边形,或以AB、BE、AD的延长线为边构造梯形也可以得证.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 已知:如图所示,以梯形ABCD的对角线AC及腰AD为邻边作平行四边形ACED,连接EB,DC的延长线交BE于F.求证:EF=BF.
已知:如图所示,以梯形ABCD的对角线AC及腰AD为邻边作平行四边形ACED,连接EB,DC的延长线交BE于F.求证:EF=BF.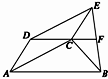 (几何证明选讲选做题)已知:如图所示,以梯形ABCD的对角线AC及腰AD为邻边作平行四边形ACED,连接EB,DC的延长线交BE于F.
(几何证明选讲选做题)已知:如图所示,以梯形ABCD的对角线AC及腰AD为邻边作平行四边形ACED,连接EB,DC的延长线交BE于F.