题目内容
 已知:如图所示,以梯形ABCD的对角线AC及腰AD为邻边作平行四边形ACED,连接EB,DC的延长线交BE于F.求证:EF=BF.
已知:如图所示,以梯形ABCD的对角线AC及腰AD为邻边作平行四边形ACED,连接EB,DC的延长线交BE于F.求证:EF=BF.分析:已知梯形ABCD,可得DC∥AB,可再做一条平行线来构造平行四边形,得到F为新平行四边形的对角线的交点,从而可得结论.
解答:证明:过点B作BG∥AD,交DC的延长线于G,连接EG.
∵DC∥AB,
∴四边形ABGD是平行四边形,
∴BG平行且等于AD.
在平行四边形ACED中,AD∥CE且AD=CE,
∴CE∥BG且CE=BG.
∴四边形BCEG为平行四边形.
∴EF=BF.

∵DC∥AB,
∴四边形ABGD是平行四边形,
∴BG平行且等于AD.
在平行四边形ACED中,AD∥CE且AD=CE,
∴CE∥BG且CE=BG.
∴四边形BCEG为平行四边形.
∴EF=BF.
点评:本题考查了平行四边形的判定与性质,三角形的问题通常也转换为平行四边形的问题来解决,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目


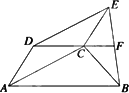
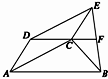 (几何证明选讲选做题)已知:如图所示,以梯形ABCD的对角线AC及腰AD为邻边作平行四边形ACED,连接EB,DC的延长线交BE于F.
(几何证明选讲选做题)已知:如图所示,以梯形ABCD的对角线AC及腰AD为邻边作平行四边形ACED,连接EB,DC的延长线交BE于F.