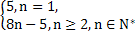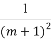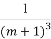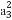题目内容
已知{an}是各项均为正数的等比数列,且a1+a2=2(
+
),a3+a4+a5=64(
+
+
),
(1)求{an}的通项公式.
(2)设bn=(an+
)2,求数列{bn}的前n项和Tn.
(1) an=2n-1 (2) Tn=
(4n-41-n)+2n+1.
【解析】【思路点拨】(1)设出公比根据条件列出关于a1与q的方程组求得a1与q,即可求得数列的通项公式.
(2)由(1)中求得数列的通项公式,可求出{bn}的通项公式,由其通项公式可知分开求和即可.
【解析】
(1)设公比为q,则an=a1qn-1.由已知得
化简得
又a1>0,故q=2,a1=1,所以an=2n-1.
(2)由(1)得bn=(an+
)2=
+2+
=4n-1+
+2.
所以Tn=(1+4+…+4n-1)+(1+
+…+)+2n
=
+
+2n
=(4n-41-n)+2n+1.
练习册系列答案
相关题目
