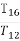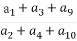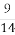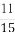Question

知{an}是首项为-2的等比数列,Sn是其前n项和,且S3,S2,S4成等差数列,

(1)求数列{an}的通项公式.

(2)若bn=log2|an|,求数列{}的前n项和Tn.

 

Answer 1

(1) an=(-2)n (2) Tn=1-=

【解析】(1)设数列{an}的公比为q,其首项a1=-2.

方法一:①若q=1,则Sn=na1=-2n,

此时S3=-6,S2=-4,S4=-8,S3,S2,S4不成等差数列,不合题意;

②若q≠1,则Sn==-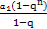

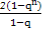
因为S3,S2,S4成等差数列,

所以2S2=S3+S4,即-=--,

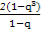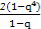整理得q2+q-2=0,

解得q=-2或q=1(舍去),

综上所述,数列{an}的通项公式为an=a1qn-1

=(-2)×(-2)n-1=(-2)n.

方法二:S2=a1+a1q,S3=a1+a1q+a1q2,S4=a1+a1q+a1q2+a1q3.

因为S3,S2,S4成等差数列,

所以2S2=S3+S4,即2a1+2a1q=2a1+2a1q+2a1q2+a1q3,整理得2a1q2+a1q3=0.

因为a1≠0,q≠0,所以q=-2,

故数列{an}的通项公式为an=a1qn-1=(-2)×(-2)n-1=(-2)n.

(2)由(1)可知an=(-2)n,

依题意bn=log2|an|=log2|(-2)n|=log22n=n,

所以==-,

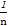所以Tn=(1-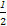)+(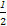-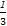)+…+(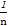-)=1-=.