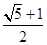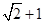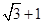题目内容
给出如下四个命题:
①方程x2+y2-2x+1=0表示的图形是圆;
②若椭圆的离心率为
,则两个焦点与短轴的两个端点构成正方形;
③抛物线x=2y2的焦点坐标为(
,0);
④双曲线
-
=1的渐近线方程为y=±
x.
其中正确命题的序号是______.
①方程x2+y2-2x+1=0表示的图形是圆;
②若椭圆的离心率为
| ||
| 2 |
③抛物线x=2y2的焦点坐标为(
| 1 |
| 8 |
④双曲线
| y2 |
| 49 |
| x2 |
| 25 |
| 5 |
| 7 |
其中正确命题的序号是______.
对①,(x-1)2+y2=0,∴x=1,y=0,
即表示点(1,0).
对②,若e=
=
,则b=C、
∴两焦点与短轴两端点构成正方形.
对③,抛物线方程为y2=
x,其焦点坐标为(
,0).
对④,双曲线
-
=1的渐近线方程为
±
=0,
即y=±
x.
故答案为 ②③
即表示点(1,0).
对②,若e=
| c |
| a |
| ||
| 2 |
∴两焦点与短轴两端点构成正方形.
对③,抛物线方程为y2=
| 1 |
| 2 |
| 1 |
| 8 |
对④,双曲线
| y2 |
| 49 |
| x2 |
| 25 |
| y |
| 7 |
| x |
| 5 |
即y=±
| 7 |
| 5 |
故答案为 ②③

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目