题目内容

设椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点为F，C为椭圆短轴上的端点，向量
FC
绕F点顺时针旋转90°后得到向量
FC′
，其中C′点恰好落在椭圆右准线上，则该椭圆的离心率为______．
设F（c，0），C（0，b）
由题意可知|FC|=|FC'|∠CFC'=90° 所以△CFC'是等腰直角三角形
∴|FC|=|FC'|=a
∵∠CFC'=90°
∴|CC'|=
2
a
∴右准线为x=
a2
c
=
2
a 即
a
c
=
2

∴离心率e=
2
2

故答案为
2
2
．
练习册系列答案
相关题目
在平面直角坐标系xOy中，已知椭圆
x2
4
+
y2
3
=1的左焦点为F，直线x-y-1=0，x-y+1=0与椭圆分别相交于点A，B，C，D，则AF+BF+CF+DF=______．
点A、B分别是椭圆
x2
36
+
y2
20
=1长轴的左、右焦点，点F是椭圆的右焦点．点P在椭圆上，且位于x轴上方，PA⊥PF．
（1）求P点的坐标；
（2）设M是椭圆长轴AB上的一点，M到直线AP的距离等于|MB|，求椭圆上的点到点M的距离d的最小值．
如图，面ABC⊥α，D为AB的中点，|AB|=2，∠CDB=60°，P为α内的动点，且P到直线CD的距离为
3
，则∠APB的最大值为（　　）
A．30°B．60°C．90°D．120°
椭圆
x2
9
+
y2
2
=1的焦点为F1、F2，点P在椭圆上，若|PF1|=4，则|PF2|=______，∠F1PF2的大小为______．
定点N（1，0），动点A、B分别在图中抛物线y2=4x及椭圆
x2
4
+
y2
3
=1的实线部分上运动，且AB∥x轴，则△NAB的周长l取值范围是（　　）
A．（
2
3
，2）		B．（
10
3
，4）		C．（
51
16
，4）		D．（2，4）
给出如下四个命题：
①方程x2+y2-2x+1=0表示的图形是圆；
②若椭圆的离心率为
2
2
，则两个焦点与短轴的两个端点构成正方形；
③抛物线x=2y2的焦点坐标为（
1
8
，0）；
④双曲线
y2
49
-
x2
25
=1的渐近线方程为y=±
5
7
x．
其中正确命题的序号是______．
已知命题p：方程
x2
k-4
+
y2
k-6
=1表示双曲线；命题q：过点M（2，1）的直线与椭圆
x2
5
+
y2
k
=1恒有公共点，若p与q中有且仅有一个为真命题，求k的取值范围．
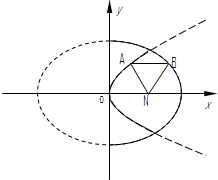
已知双曲线方程为，则双曲线的渐近线方程为(         ).
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网