题目内容
已知向量m=(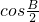 ,
, )与向量n=(
)与向量n=( ,
,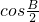 )共线,其中A、B、C是△ABC的内角.
)共线,其中A、B、C是△ABC的内角.
(1)求角B的大小;
(2)求2sin2A+cos(C-A)的取值范围.
解:(1)∵ =(
=(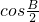 ,
, )与
)与 =(
=( ,
,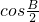 )共线,
)共线,
∴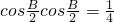 .
.
∴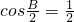 .
.
又0<B<π,
∴0< <
< ,
, .
.
∴ ,即
,即 .
.
(2)由(1)知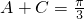 ,
,
∴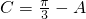 .
.
∴2sin2A+cos(C-A)=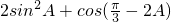 =
=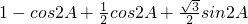 =
=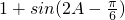 .
.
∵0<A< ,
,
∴ <
< <
< .
.
∴ ∈(
∈( ,1).
,1).
∴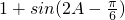 ∈(
∈( ,2),
,2),
即2sin2A+cos(C-A)的取值范围是( ,2).
,2).
分析:(1)先根据向量的共线可得到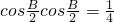 ,进而可得到
,进而可得到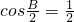 ,再由B是△ABC的内角确定B的范围从而可确定
,再由B是△ABC的内角确定B的范围从而可确定 的范围得到cos
的范围得到cos 的值,最后得到B的值.
的值,最后得到B的值.
(2)由(1)知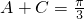 从而可得到
从而可得到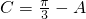 ,然后代入到2sin2A+cos(C-A)中运用两角和与差的公式进行化简得到2sin2A+cos(C-A)=
,然后代入到2sin2A+cos(C-A)中运用两角和与差的公式进行化简得到2sin2A+cos(C-A)=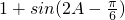 ,再结合A的范围可得到2sin2A+cos(C-A)的取值范围.
,再结合A的范围可得到2sin2A+cos(C-A)的取值范围.
点评:本题主要考查二倍角公式和向量的共线问题.考查基础知识的综合运用.
 =(
=(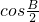 ,
, )与
)与 =(
=( ,
,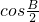 )共线,
)共线,∴
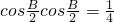 .
.∴
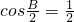 .
.又0<B<π,
∴0<
 <
< ,
, .
.∴
 ,即
,即 .
.(2)由(1)知
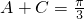 ,
,∴
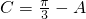 .
.∴2sin2A+cos(C-A)=
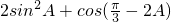 =
=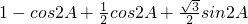 =
=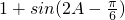 .
.∵0<A<
 ,
,∴
 <
< <
< .
.∴
 ∈(
∈( ,1).
,1).∴
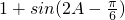 ∈(
∈( ,2),
,2),即2sin2A+cos(C-A)的取值范围是(
 ,2).
,2).分析:(1)先根据向量的共线可得到
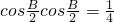 ,进而可得到
,进而可得到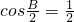 ,再由B是△ABC的内角确定B的范围从而可确定
,再由B是△ABC的内角确定B的范围从而可确定 的范围得到cos
的范围得到cos 的值,最后得到B的值.
的值,最后得到B的值.(2)由(1)知
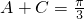 从而可得到
从而可得到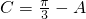 ,然后代入到2sin2A+cos(C-A)中运用两角和与差的公式进行化简得到2sin2A+cos(C-A)=
,然后代入到2sin2A+cos(C-A)中运用两角和与差的公式进行化简得到2sin2A+cos(C-A)=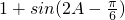 ,再结合A的范围可得到2sin2A+cos(C-A)的取值范围.
,再结合A的范围可得到2sin2A+cos(C-A)的取值范围.点评:本题主要考查二倍角公式和向量的共线问题.考查基础知识的综合运用.

练习册系列答案
相关题目