题目内容
 如图,若正四棱柱ABCD-A1B1C1D1的底面边长为1,高为
如图,若正四棱柱ABCD-A1B1C1D1的底面边长为1,高为| 2 |
分析:根据正四棱柱的几何特征,我们易根据AD∥BC,得到∠D1BC即为异面直线BD1与AD所成角,根据已知中正四棱柱ABCD-A1B1C1D1的底面边长为1,高为
,求出△D1BC中各边的长,解△D1BC即可得到答案.
| 2 |
解答:解:∵AD∥BC
∴∠D1BC即为异面直线BD1与AD所成角
连接D1C,在△D1BC中,
∵正四棱柱ABCD-A1B1C1D1的底面边长为1,高为
,
∴D1B=2,BC=1,D1C=
∴cos∠D1BC=
即∠D1BC=60°
故异面直线BD1与AD所成角的大小是60°
故答案为:60°
∴∠D1BC即为异面直线BD1与AD所成角
连接D1C,在△D1BC中,
∵正四棱柱ABCD-A1B1C1D1的底面边长为1,高为
| 2 |
∴D1B=2,BC=1,D1C=
| 3 |
∴cos∠D1BC=
| 1 |
| 2 |
即∠D1BC=60°
故异面直线BD1与AD所成角的大小是60°
故答案为:60°
点评:本题考查的知识点是异面直线及其所成的角,其中根据已知条件确定找到两条异面直线夹角是解答本题的关键.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
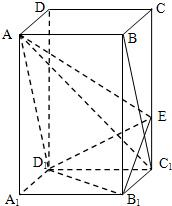 如图,在正四棱柱ABCD-A1B1C1D1中,
如图,在正四棱柱ABCD-A1B1C1D1中,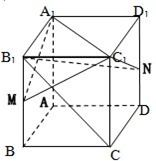 如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M、N分别是棱BB1,DD1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M、N分别是棱BB1,DD1的中点. 如图,在正四棱柱ABCD-A1B1C1D1中,已知AB=2,AA1=
如图,在正四棱柱ABCD-A1B1C1D1中,已知AB=2,AA1= (2008•奉贤区二模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=4,AA1=8.
(2008•奉贤区二模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=4,AA1=8. ,M为棱A1A上的点,若A1C⊥平面MB1D1.
,M为棱A1A上的点,若A1C⊥平面MB1D1.