题目内容
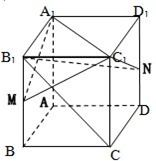 如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M、N分别是棱BB1,DD1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M、N分别是棱BB1,DD1的中点.①求异面直线A1M与B1C所成的角的余弦值;
②若正四棱柱ABCD-A1B1C1D1的体积为V,三棱锥N-A1B1C1的体积为V1,求
| V1 | V |
③求平面A1MC1与平面B1NC1所成的二面角的大小.
分析:①先将B1C平移到A1D,根据异面直线所成角的定义可知∠MA1D是异面直线A1M与B1C所成的角(或补角),然后利用余弦定理求出此角的余弦值即可;
②先利用正棱柱的体积公式求出正四棱柱ABCD-A1B1C1D1的体积为V,然后利用三棱锥的体积公式求出三棱锥N-A1B1C1的体积,即可求出所求;
③取AA1中点P,连接B1P、NP、MP,则四边形B1MPA1为正方形,根据A1M⊥B1P,A1M⊥B1C1,满足线面垂直的判定定理可知A1M⊥平面B1NC1,而A1M?平面A1MC1,满足面面垂直的判定定理可知平面A1MC1⊥平面B1NC,从而求出平面A1MC1与平面B1NC1所成二面角大小.
②先利用正棱柱的体积公式求出正四棱柱ABCD-A1B1C1D1的体积为V,然后利用三棱锥的体积公式求出三棱锥N-A1B1C1的体积,即可求出所求;
③取AA1中点P,连接B1P、NP、MP,则四边形B1MPA1为正方形,根据A1M⊥B1P,A1M⊥B1C1,满足线面垂直的判定定理可知A1M⊥平面B1NC1,而A1M?平面A1MC1,满足面面垂直的判定定理可知平面A1MC1⊥平面B1NC,从而求出平面A1MC1与平面B1NC1所成二面角大小.
解答:解:①∵A1D∥B1C
∴∠MA1D是异面直线A1M与B1C所成的角(或补角)
MA1=
a,A1D=
a,MD=
a
cos∠MA1D=
=
=
所以异面直线A1M与B1C所成的角余弦值为
②V=2a3,
VN-A1B1C1=
a×
a2=
a3,
=
③取AA1中点P,连接B1P、NP、MP,则四边形B1MPA1为正方形.
∵A1M⊥B1P,且B1C1⊥平面A1B1BA,
∴B1C1⊥A1M,即A1M⊥B1C1,
∴A1M⊥平面B1PNC1
即A1M⊥平面B1NC1,
∵A1M?平面A1MC1,
所以,平面A1MC1⊥平面B1NC.
故平面A1MC1与平面B1NC1所成二面角大小为90°.
∴∠MA1D是异面直线A1M与B1C所成的角(或补角)
MA1=
| 2 |
| 5 |
| 3 |
cos∠MA1D=
| A1M2+A1D2-MD2 |
| 2A1M•A1D |
=
| 2a2+5a2-3a2 | ||||
2×
|
=
| ||
| 5 |
所以异面直线A1M与B1C所成的角余弦值为
| ||
| 5 |
②V=2a3,
VN-A1B1C1=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| V1 |
| V |
| 1 |
| 12 |
③取AA1中点P,连接B1P、NP、MP,则四边形B1MPA1为正方形.
∵A1M⊥B1P,且B1C1⊥平面A1B1BA,
∴B1C1⊥A1M,即A1M⊥B1C1,
∴A1M⊥平面B1PNC1
即A1M⊥平面B1NC1,
∵A1M?平面A1MC1,
所以,平面A1MC1⊥平面B1NC.
故平面A1MC1与平面B1NC1所成二面角大小为90°.
点评:本题主要考查了异面直线所成角的度量,以及体积的求解和面面垂直的判定,同时考查了计算能力和推理能力,属于中档题.

练习册系列答案
相关题目
 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
 如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点.
如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点. (2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,
(2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a, 如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点. (2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )
(2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )