题目内容
14.图中(1)(2)(3)(4)四个图象各表示两个变量x,y的对应关系,其中表示y是x的函数关系的有②③.
分析 根据函数的概念,直线x=a与函数的图象至多有1个交点,可判断出答案.
解答 解:∵由函数的概念,直线x=a与函数的图象至多有1个交点,
∴①④不符合题意,②③符合题意
故答案为:②③.
点评 本题考查了函数的概念,运用图象求解判断,体现了数形结合的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.奇函数f(x)当x∈(0,+∞)时的解析式为f(x)=x2-x+2,则f(-1)=( )
| A. | -2 | B. | 2 | C. | 4 | D. | -4 |
9.已知关于x的方程4x2-2(m+1)x+m=0的两个根恰好是一个直角三角形的两个锐角的余弦值,实数m的值( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
19.下列各组函数中,表示同一个函数的是( )
| A. | $f(x)=x,g(x)={(\sqrt{x})^2}$ | B. | $f(x)=x,g(x)=\sqrt{x^2}$ | ||
| C. | $f(x)=\frac{{{x^2}-9}}{x-3},g(x)=x+3$ | D. | f(x)=x2+1,g(t)=t2+1 |
6.若函数f(x)=loga(2x2+x)(a>0且a≠1)在区间(0,$\frac{1}{2}$)内恒有f(x)>0,则f(x)的单调递增区间为( )
| A. | (-∞,$\frac{1}{4}$) | B. | (-$\frac{1}{4}$,+∞) | C. | (0,+∞) | D. | (-∞,-$\frac{1}{2}$) |
3.若${∫}_{\;}^{\;}$${\;}_{0}^{T}$x2dx=9,则常数T的值为( )
| A. | 9 | B. | -3 | C. | 3 | D. | 1 |
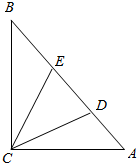 如图,在Rt△ABC中,∠A=60°,AB=6,点D、E是斜边AB上两点.
如图,在Rt△ABC中,∠A=60°,AB=6,点D、E是斜边AB上两点.