题目内容
17.已知{a,b,c}?P⊆{a,b,c,d,e,f},则满足该条件的集合P有7个.分析 集合A一定要含有a、b、c三个元素,且至少要多一个,多的元素只能从d、e、f中选,推出集合A可以是下面7个集合.
解答 解:A可以为{a,b,c,d},{a,b,c,e},{a,b,c,f},{a,b,c,d,e},{a,b,c,d,f},{a,b,c,e,f},
{a,b,c,d,e,f},个数为7.
故答案为:7.
点评 子集包括真子集和它本身,集合的子集个数问题,对于集合M的子集问题一般来说,若M中有n个元素,则集合M的子集共有2n个,真子集2n-1个.

练习册系列答案
相关题目
8.已知向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(sinα,cosα),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则sinαcosα=( )
| A. | $\frac{12}{25}$ | B. | -$\frac{12}{25}$ | C. | -$\frac{9}{25}$ | D. | $\frac{9}{25}$ |
2.已知全集U=R,A={x|-2<x<2},B={x|x2-3x-4≤0},则∁U(A∩B)=( )
| A. | {x|-1≤x<2} | B. | {x|x<-1或x≥2} | C. | {x|-1≤x≤4} | D. | {x|x>4或x<1} |
6.已知函数f(x)=sin(2x-$\frac{π}{6}$),则下面说法正确的是( )
| A. | 函数图象关于点($\frac{π}{12}$,0)对称 | B. | 函数图象的-条对称轴方程为x=$\frac{π}{6}$ | ||
| C. | 函数f(x)是奇函数 | D. | 函数f(x)是偶函数 |
7.若数列{an}的通项公式为an=$\frac{1}{3}$(10n-1),则{an}的前n项和为( )
| A. | $\frac{1{0}^{n+1}-10}{27}$-$\frac{n}{3}$ | B. | $\frac{1{0}^{n}-1}{9}$-$\frac{n}{3}$ | C. | $\frac{1{0}^{n}-n-1}{9}$ | D. | $\frac{1{0}^{n}}{9}$ |
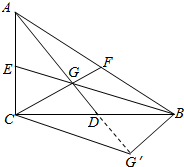 如图,在△ABC中,G为重心,在AD的延长线上取一点G′,使得GD=G′D=4,若CG=6,BG=10,求△ABC的面积.
如图,在△ABC中,G为重心,在AD的延长线上取一点G′,使得GD=G′D=4,若CG=6,BG=10,求△ABC的面积.