题目内容
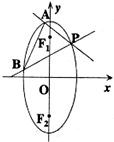 已知椭圆两焦点F1、F2在y轴上,短轴长为2
已知椭圆两焦点F1、F2在y轴上,短轴长为2| 2 |
| ||
| 2 |
| PF1 |
| PF2 |
(1)求P点坐标;
(2)求证直线AB的斜率为定值.
分析:(1)设出椭圆的标准方程,根据题意可知b,进而根据离心率和a,b和c的关系求得a和c,则椭圆的方程可得.进而求得焦点的坐标,设出点P的坐标,分别表示出
和
,进而根据
•
=1求得x0和y0的关系式,把点P的坐标代入椭圆方程求和另一个关系式,联立方程求得x0和y0即P的坐标.
(2)根据(1)可知PF1∥x轴,设PB的斜率为k,根据点斜式表示出直线的方程,与椭圆的方程联立消去y,设出B的坐标,根据题意可求得xB的表达式,同理求得xA的表达式,进而可知xA-xB的表达式,根据直线方程求得yA-yB,进而根据斜率公式求得直线AB的斜率,结果为定值.
| PF 1 |
| PF 2 |
| PF1 |
| PF2 |
(2)根据(1)可知PF1∥x轴,设PB的斜率为k,根据点斜式表示出直线的方程,与椭圆的方程联立消去y,设出B的坐标,根据题意可求得xB的表达式,同理求得xA的表达式,进而可知xA-xB的表达式,根据直线方程求得yA-yB,进而根据斜率公式求得直线AB的斜率,结果为定值.
解答:解:(1)设椭圆的方程为
+
=1,由题意可得b=
,
=
,即a=
c,
∵a2-c2=2
∴c=
,a=2
∴椭圆方程为
+
=1
∴焦点坐标为(0,
),(0,-
),设p(x0,y0)(x0>0,y0>0)
则
=(-x0,
-y0),
=(-x0,-
-y0),
∴
•
=x02-(2-y02)=1
∵点P在曲线上,则
+
=1
∴x02=
,
从而
-(2-y02)=1,得y0=
,则点P的坐标为(1,
)
(2)由(1)知PF1∥x轴,直线PA,PB斜率互为相反数,设PB的斜率为k(k>0),
则PB的直线方程为y-
=k(x-1),由
得
(2+k2)x2+2k(
-k)x+(
-k2)-4=0
设B(xB,yB),则xB=
-1=
,
同理可得xA=
,则xA-xB=
,
yA-yB=-k(xA-1)-k(xB-1)=
所以AB的斜率kAB=
=
为定值.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| c |
| a |
| ||
| 2 |
| 2 |
∵a2-c2=2
∴c=
| 2 |
∴椭圆方程为
| x2 |
| 2 |
| y2 |
| 4 |
∴焦点坐标为(0,
| 2 |
| 2 |
则
| PF1 |
| 2 |
| PF2 |
| 2 |
∴
| PF1 |
| PF2 |
∵点P在曲线上,则
| y02 |
| 4 |
| x02 |
| 2 |
∴x02=
4-
| ||
| 2 |
从而
4-
| ||
| 2 |
| 2 |
| 2 |
(2)由(1)知PF1∥x轴,直线PA,PB斜率互为相反数,设PB的斜率为k(k>0),
则PB的直线方程为y-
| 2 |
|
(2+k2)x2+2k(
| 2 |
| 2 |
设B(xB,yB),则xB=
2k(k-
| ||
| 2+k2 |
k2 -2
| ||
| 2+k2 |
同理可得xA=
k2+2
| ||
| 2+k2 |
4
| ||
| 2+k2 |
yA-yB=-k(xA-1)-k(xB-1)=
| 8k |
| 2+k2 |
所以AB的斜率kAB=
| yA-yB |
| xA-xB |
| 2 |
点评:本题主要考查了椭圆的应用,直线与椭圆的关系,椭圆的标准方程.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,离心率为
,离心率为 ,P是椭圆在第一象限弧上一点,且
,P是椭圆在第一象限弧上一点,且 ,过P作关于直线F1P对称的两条直线PA、PB分别交椭圆于A、B两点。
,过P作关于直线F1P对称的两条直线PA、PB分别交椭圆于A、B两点。 ,离心率为
,离心率为 ,P是椭圆在第一象限弧上一点,且
,P是椭圆在第一象限弧上一点,且 ,过P作关于直线F1P对称的两条直线PA、PB分别交椭圆于A、B两点.
,过P作关于直线F1P对称的两条直线PA、PB分别交椭圆于A、B两点.
 ,离心率为
,离心率为 ,P是椭圆在第一象限弧上一点,且
,P是椭圆在第一象限弧上一点,且 ,过P作关于直线F1P对称的两条直线PA、PB分别交椭圆于A、B两点.
,过P作关于直线F1P对称的两条直线PA、PB分别交椭圆于A、B两点.