题目内容
已知椭圆两焦点F1、F2在y轴上,短轴长为2 ,离心率为
,离心率为 ,P是椭圆在第一象限弧上一点,且
,P是椭圆在第一象限弧上一点,且 ,过P作关于直线F1P对称的两条直线PA、PB分别交椭圆于A、B两点。
,过P作关于直线F1P对称的两条直线PA、PB分别交椭圆于A、B两点。
(1)求P点坐标;
(2)求证直线AB的斜率为定值。
 ,离心率为
,离心率为 ,P是椭圆在第一象限弧上一点,且
,P是椭圆在第一象限弧上一点,且 ,过P作关于直线F1P对称的两条直线PA、PB分别交椭圆于A、B两点。
,过P作关于直线F1P对称的两条直线PA、PB分别交椭圆于A、B两点。(1)求P点坐标;
(2)求证直线AB的斜率为定值。
解:(1)设椭圆方程为 由题意可知  方程为   设  则  ∴  ∵点  在曲线上 在曲线上则  ∴  从而  得 得 则点P的坐标为  。 。(2)由(1)知  轴,直线PA、PB斜率互为相反数, 轴,直线PA、PB斜率互为相反数,设PB斜率为  , ,则PB的直线方程为:  由  得 得 设  则  同理可得  则   所以:AB的斜率  为定值。 为定值。 |
 |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
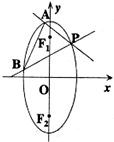 已知椭圆两焦点F1、F2在y轴上,短轴长为
已知椭圆两焦点F1、F2在y轴上,短轴长为 ,离心率为
,离心率为 ,P是椭圆在第一象限弧上一点,且
,P是椭圆在第一象限弧上一点,且 ,过P作关于直线F1P对称的两条直线PA、PB分别交椭圆于A、B两点.
,过P作关于直线F1P对称的两条直线PA、PB分别交椭圆于A、B两点.
 ,离心率为
,离心率为 ,P是椭圆在第一象限弧上一点,且
,P是椭圆在第一象限弧上一点,且 ,过P作关于直线F1P对称的两条直线PA、PB分别交椭圆于A、B两点.
,过P作关于直线F1P对称的两条直线PA、PB分别交椭圆于A、B两点.