题目内容
已知函数 ,其中a∈R.
,其中a∈R.(Ⅰ)当a=1时,求曲线y=f(x)在原点处的切线方程;
(Ⅱ)求f(x)的单调区间.
【答案】分析:(Ⅰ)当a=1时,求导函数,确定切点坐标与切线的斜率,即可得到曲线y=f(x)在原点处的切线方程;
(Ⅱ)求导函数可得,分类讨论,利用导数的正负,可得函数的单调区间.
解答:解:(Ⅰ)当a=1时, ,
, . …(2分)
. …(2分)
∴f'(0)=2,
∵f(0)=0,
∴曲线y=f(x)在原点处的切线方程是2x-y=0.…(4分)
(Ⅱ)求导函数可得, . …(6分)
. …(6分)
当a=0时, ,所以f(x)在(0,+∞)单调递增,在(-∞,0)单调递减. …(7分)
,所以f(x)在(0,+∞)单调递增,在(-∞,0)单调递减. …(7分)
当a≠0, .
.
①当a>0时,令f'(x)=0,得x1=-a, ,f(x)与f'(x)的情况如下:
,f(x)与f'(x)的情况如下:
故f(x)的单调减区间是(-∞,-a), ;单调增区间是
;单调增区间是 .…(10分)
.…(10分)
②当a<0时,f(x)与f'(x)的情况如下:
所以f(x)的单调增区间是 ;单调减区间是
;单调减区间是 ,(-a,+∞).…(13分)
,(-a,+∞).…(13分)
综上,a>0时,f(x)在(-∞,-a), 单调递减;在
单调递减;在 单调递增.a=0时,f(x)在(0,+∞)单调递增,在(-∞,0)单调递减;a<0时,f(x)在
单调递增.a=0时,f(x)在(0,+∞)单调递增,在(-∞,0)单调递减;a<0时,f(x)在 ,(-a,+∞)单调递增;在
,(-a,+∞)单调递增;在 单调递减.
单调递减.
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查分类讨论的数学思想,属于中档题.
(Ⅱ)求导函数可得,分类讨论,利用导数的正负,可得函数的单调区间.
解答:解:(Ⅰ)当a=1时,
 ,
, . …(2分)
. …(2分)∴f'(0)=2,
∵f(0)=0,
∴曲线y=f(x)在原点处的切线方程是2x-y=0.…(4分)
(Ⅱ)求导函数可得,
 . …(6分)
. …(6分)当a=0时,
 ,所以f(x)在(0,+∞)单调递增,在(-∞,0)单调递减. …(7分)
,所以f(x)在(0,+∞)单调递增,在(-∞,0)单调递减. …(7分)当a≠0,
 .
.①当a>0时,令f'(x)=0,得x1=-a,
 ,f(x)与f'(x)的情况如下:
,f(x)与f'(x)的情况如下:| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f'(x) | - | + | - | ||
| f(x) | ↘ | f(x1) | ↗ | f(x2) | ↘ |
 ;单调增区间是
;单调增区间是 .…(10分)
.…(10分)②当a<0时,f(x)与f'(x)的情况如下:
| x | (-∞,x2) | x2 | (x2,x1) | x1 | (x1,+∞) |
| f'(x) | + | - | + | ||
| f(x) | ↗ | f(x2) | ↘ | f(x1) | ↗ |
 ;单调减区间是
;单调减区间是 ,(-a,+∞).…(13分)
,(-a,+∞).…(13分)综上,a>0时,f(x)在(-∞,-a),
 单调递减;在
单调递减;在 单调递增.a=0时,f(x)在(0,+∞)单调递增,在(-∞,0)单调递减;a<0时,f(x)在
单调递增.a=0时,f(x)在(0,+∞)单调递增,在(-∞,0)单调递减;a<0时,f(x)在 ,(-a,+∞)单调递增;在
,(-a,+∞)单调递增;在 单调递减.
单调递减.点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R.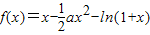 ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R.