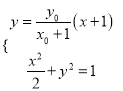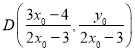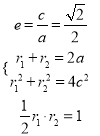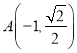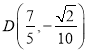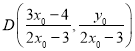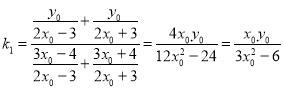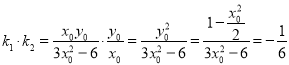题目内容
【题目】(Ⅰ)设命题![]() 实数
实数![]() 满足
满足![]() ,其中
,其中![]() ,命题
,命题![]() 实数
实数![]() 满足
满足![]() .若
.若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
(Ⅱ)已知命题![]() 方程
方程![]() 表示焦点在x轴上双曲线;命题
表示焦点在x轴上双曲线;命题![]() 空间向量
空间向量![]() ,
,![]() 的夹角为锐角,如果命题“
的夹角为锐角,如果命题“![]() ”为真,命题“
”为真,命题“![]() ”为假.求
”为假.求![]() 的取值范围;
的取值范围;
【答案】(Ⅰ)![]() (Ⅱ
(Ⅱ![]()
【解析】
(Ⅰ)由![]() 是
是![]() 的充分不必要条件,得
的充分不必要条件,得![]() 是
是![]() 的充分不必要条件,分别求出
的充分不必要条件,分别求出![]() 为真时,
为真时,![]() 的范围,进而可得出结果;
的范围,进而可得出结果;
(Ⅱ)先求出![]() 为真时,
为真时,![]() 的范围,再由命题“
的范围,再由命题“![]() ”为真,命题“
”为真,命题“![]() ”为假,得到命题
”为假,得到命题![]() 有且仅有一个是真命题,进而可求出结果.
有且仅有一个是真命题,进而可求出结果.
(Ⅰ)![]() 是
是![]() 的充分不必要条件,即
的充分不必要条件,即![]() 是
是![]() 的充分不必要条件,
的充分不必要条件,
命题![]() 实数
实数![]() 满足
满足![]() ,其中
,其中![]() 为真,可得
为真,可得![]() ,
,
命题![]() 实数
实数![]() 满足
满足![]() 为真,可得
为真,可得![]() ,即
,即![]() ;
;
即![]() ,则
,则![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() ;
;
(Ⅱ)命题![]() 为真的条件是:
为真的条件是:![]() 且
且![]() ,解得
,解得![]() ;
;
命题![]() 空间向量
空间向量![]() ,
,![]() 的夹角为锐角,为真,
的夹角为锐角,为真,
即有![]() ,即
,即![]() ,解得
,解得![]() ,
,
由于![]() 不共线,可得
不共线,可得![]() .
.
又命题“![]() ”为真,命题“
”为真,命题“![]() ”为假,
”为假,
可得命题![]() 有且仅有一个是真命题,
有且仅有一个是真命题,
即![]() 或
或![]() ,
,
即有![]() .
.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目