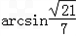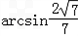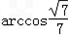题目内容
已知球O的表面积为4π,A、B、C三点都在球面上,且A与B、A与C,B与C两点的球面距离分别是
,
,
,则OB与平面ABC所成的角是( )
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
分析:由题意,球的半径为1,根据A与B、A与C,B与C两点的球面距离分别是
,
,
,可得∠AOB=
,∠AOC=
,∠BOC=
,
,从而可求AB=AC=
,BC=1,可求VA-OBC=
×
×1=
,利用等体积法求出O到平面ABC的距离,即可求得结论.
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| 2 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 12 |
解答:解:由题意,∵球O的表面积为4π,
∴球的半径为1,
∵A与B、A与C,B与C两点的球面距离分别是
,
,
,
∴∠AOB=
,∠AOC=
,∠BOC=
,∴AO⊥面BOC
∵OA=OB=OC=1,∴AB=AC=
,BC=1.
∴VA-OBC=
×
×1=
设h为O到平面ABC的距离,则
∵S△ABC=
×1×
=
∴VA-OBC=VO-ABC=
×
h=
∴h=
∴OA与平面ABC所成角的正弦值为
∴OB与平面ABC所成的角是arcsin
故选A.
∴球的半径为1,
∵A与B、A与C,B与C两点的球面距离分别是
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
∴∠AOB=
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
∵OA=OB=OC=1,∴AB=AC=
| 2 |
∴VA-OBC=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 12 |
设h为O到平面ABC的距离,则
∵S△ABC=
| 1 |
| 2 |
2-
|
| ||
| 4 |
∴VA-OBC=VO-ABC=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 12 |
∴h=
| ||
| 7 |
∴OA与平面ABC所成角的正弦值为
| ||
| 7 |
∴OB与平面ABC所成的角是arcsin
| ||
| 7 |
故选A.
点评:本题考查线面角,考查三棱锥的体积,解题的关键是利用等体积求出点到面的距离,属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
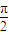 ,
,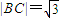 ,则球心O到平面ABC的距离为( )
,则球心O到平面ABC的距离为( )
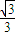
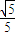
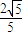
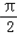 ,
,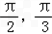 ,则OB与平面ABC所成的角是
,则OB与平面ABC所成的角是