题目内容
如图所示，正方形AA1D1D与矩形ABCD所在平面互相垂直，AB=2AD=2，点E为AB的中点．
（1）求证：BD1∥平面A1DE；
（2）求证：D1E⊥A1D；
（3）（文）求D1E与平面A1DE所成角的大小．
证明：（1）四边形ADD1A1为正方形，O是AD1的中点，点E为AB的中点，连接OE．
∴EO为△ABD1的中位线
∴EO∥BD1…（2分）
又∵BD1?平面A1DE，OE?平面A1DE
∴BD1∥平面A1DE…（4分）
（2）由已知可得：AB⊥平面ADD1A1，A1D?平面ADD1A1
∴AB⊥A1D，
∵正方形AA1D1D
∴A1D⊥AD1，
AB∩AD1=A
∴A1D⊥平面AD1E，D1E?平面AD1E
∴A1D⊥D1E…．（4分）
（3）（文科）∵
∴
∴
∵
设D1E与平面A1DE所成角为α
∴
∴
…（6分）
分析：（1）四边形ADD1A1为正方形，O是AD1的中点，点E为AB的中点，连接OE，所以EO为△ABD1的中位线，从而有EO∥BD1，利用线面平行的判定定理可证BD1∥平面A1DE；
（2）由已知可得：AB⊥平面ADD1A1，从而可知AB⊥A1D，所以A1D⊥平面A1DE，从而有A1D⊥D1E；
（3）利用等体积先求出D1到平面A1DE的距离，设D1E与平面A1DE所成角为α，利用正弦函数可求D1E与平面A1DE所成角．
点评：本题以面面垂直为载体，考查线面位置关系，考查线面角，综合性强．
∴EO为△ABD1的中位线
∴EO∥BD1…（2分）
又∵BD1?平面A1DE，OE?平面A1DE
∴BD1∥平面A1DE…（4分）
（2）由已知可得：AB⊥平面ADD1A1，A1D?平面ADD1A1
∴AB⊥A1D，
∵正方形AA1D1D
∴A1D⊥AD1，
AB∩AD1=A
∴A1D⊥平面AD1E，D1E?平面AD1E
∴A1D⊥D1E…．（4分）
（3）（文科）∵
∴
∴
∵
设D1E与平面A1DE所成角为α
∴
∴
…（6分）
分析：（1）四边形ADD1A1为正方形，O是AD1的中点，点E为AB的中点，连接OE，所以EO为△ABD1的中位线，从而有EO∥BD1，利用线面平行的判定定理可证BD1∥平面A1DE；
（2）由已知可得：AB⊥平面ADD1A1，从而可知AB⊥A1D，所以A1D⊥平面A1DE，从而有A1D⊥D1E；
（3）利用等体积先求出D1到平面A1DE的距离，设D1E与平面A1DE所成角为α，利用正弦函数可求D1E与平面A1DE所成角．
点评：本题以面面垂直为载体，考查线面位置关系，考查线面角，综合性强．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
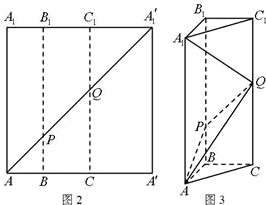如图2所示，在边长为12的正方形AA'A'1A1中，点B，C在线段AA'上，且AB=3，BC=4，作BB1∥AA1，分别交A1A'1、AA'1于点B1、P，作CC1∥AA1，分别交A1A'1、AA'1于点C1、Q，将该正方形沿BB1、CC1折叠，使得A'A1′与AA1重合，构成如图3所示的三棱柱ABC-A1B1C1．
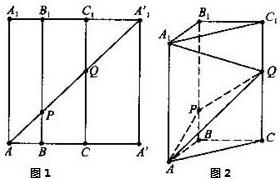如图1所示，在边长为12的正方形AA′A′1A1中，BB1∥CC1∥AA1，且AB=3，BC=4，AA′1分别交BB1，CC1于点P、Q，将该正方形沿BB1、CC1折叠，使得A′A′1与AA1重合，构成如图2所示的三棱柱ABC-A1B1C1，请在图2中解决下列问题：
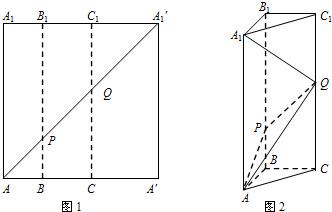如图1所示，在边长为12的正方形AA′A1′A1中，点B，C在线段AA′上，且AB=3，BC=4，作BB1∥AA1，分别交A1A1′、AA1′于点B1、P，作CC1∥AA1，分别交A1A1′、AA1′于点C1、Q，将该正方形沿BB1、CC1折叠，使得A′A1′与AA1重合，构成如图2所示的三棱柱ABC-A1B1C1．
如图，在边长为12的正方形A1 AA′A1′中，点B、C在线段AA′上，且AB = 3，BC = 4，作BB1∥AA1，分别交A1A1′、AA1′于点B1、P；作CC1∥AA1，分别交A1A1′、AA1′于点C1、Q；将该正方形沿BB1、CC1折叠，使得A′A1′ 与AA1重合，构成如图所示的三棱柱ABC—A1B1C1，在三棱柱ABC—A1B1C1中， （Ⅰ）求证：AB⊥平面BCC1B1； （Ⅱ）求面PQA与面ABC所成的锐二面角的大小．（Ⅲ）求面APQ将三棱柱ABC—A1B1C1分成上、下两部分几何体的体积之比．
