��Ŀ����
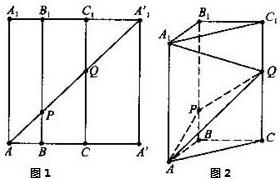 ��ͼ1��ʾ���ڱ߳�Ϊ12��������AA��A��1A1�У�BB1��CC1��AA1����AB=3��BC=4��AA��1�ֱ�BB1��CC1�ڵ�P��Q��������������BB1��CC1�۵���ʹ��A��A��1��AA1�غϣ�������ͼ2��ʾ��������ABC-A1B1C1������ͼ2�н���������⣺
��ͼ1��ʾ���ڱ߳�Ϊ12��������AA��A��1A1�У�BB1��CC1��AA1����AB=3��BC=4��AA��1�ֱ�BB1��CC1�ڵ�P��Q��������������BB1��CC1�۵���ʹ��A��A��1��AA1�غϣ�������ͼ2��ʾ��������ABC-A1B1C1������ͼ2�н���������⣺��1����֤��AB��PQ��
��2���ڵױ�AC����һ��M������AM��MC=3��4����֤��BM��ƽ��APQ��
��3����ֱ��BC��ƽ��APQ���ɽǵ�����ֵ��
��������1����AB��BC��AB��BB1����AB��ƽ��BC1����AB��PQ��
��2����M��MN��CQ��AQ��N������PN����PB��CQ��MN��PB���Ӷ��ı���PBMNΪƽ���ı��Σ��Ա�ƽ��BM��PN��������ƽ�е��ж�������BM��ƽ��APQ��
��3������ø�������꣬�Ӷ��ó���Ӧ���������꣬�����ƽ��APQ�ķ�������������ǹ�ʽ��⣮
��2����M��MN��CQ��AQ��N������PN����PB��CQ��MN��PB���Ӷ��ı���PBMNΪƽ���ı��Σ��Ա�ƽ��BM��PN��������ƽ�е��ж�������BM��ƽ��APQ��
��3������ø�������꣬�Ӷ��ó���Ӧ���������꣬�����ƽ��APQ�ķ�������������ǹ�ʽ��⣮
��� �⣺֤������1��֤������ΪAB=3��BC=4��
�⣺֤������1��֤������ΪAB=3��BC=4��
����AC=5���Ӷ�AC2=AB2+BC2��
��AB��BC����2�֣�
����ΪAB��BB1����BC��BB1=B��
����AB��ƽ��BC1����PQ?ƽ��BC1
����AB��PQ����4�֣�
��2���⣺��M��MN��CQ��AQ��N������PN��
��ΪAM��MC=3��4��AM��AC=MN��CQ=3��7��6�֣�
��MN=PB=3����PB��CQ��MN��PB�����ı���PBMNΪƽ���ı��Ρ�BM��PN������BM��ƽ��APQ��8�֣�
��3���⣺��ͼ1֪��PB=AB=3��QC=7���ֱ���BA��BC��BB1Ϊx��y��z�ᣬ
��A��3��0��0����C��0��4��0����P��0��0��3����Q��0��4��7��
=(0��4��0)��
=(-3��0��3)��
=(-3��4��7)��10�֣�
��ƽ��APQ�ķ�����Ϊ
=(a��b��c)��
����
��
��
��a=1����c=1��b=-1��cos��
��
��=
=
=-
����ֱ��BC��ƽ��APQ���ɽǵ�����ֵΪ
��12�֣�
��ע���������ⷨ����Ӧ���֣�
 �⣺֤������1��֤������ΪAB=3��BC=4��
�⣺֤������1��֤������ΪAB=3��BC=4������AC=5���Ӷ�AC2=AB2+BC2��
��AB��BC����2�֣�
����ΪAB��BB1����BC��BB1=B��
����AB��ƽ��BC1����PQ?ƽ��BC1
����AB��PQ����4�֣�
��2���⣺��M��MN��CQ��AQ��N������PN��
��ΪAM��MC=3��4��AM��AC=MN��CQ=3��7��6�֣�
��MN=PB=3����PB��CQ��MN��PB�����ı���PBMNΪƽ���ı��Ρ�BM��PN������BM��ƽ��APQ��8�֣�
��3���⣺��ͼ1֪��PB=AB=3��QC=7���ֱ���BA��BC��BB1Ϊx��y��z�ᣬ
��A��3��0��0����C��0��4��0����P��0��0��3����Q��0��4��7��
| BC |
| AP |
| AQ |
��ƽ��APQ�ķ�����Ϊ
| n |
����
|
|
��a=1����c=1��b=-1��cos��
| BC |
| n |
| ||||
|
|
| -4 | ||
4��
|
| ||
| 3 |
����ֱ��BC��ƽ��APQ���ɽǵ�����ֵΪ
| ||
| 3 |
��ע���������ⷨ����Ӧ���֣�
������������Ҫ���������ߣ������棬�������λ�ù�ϵ������ƽ�к����洹ֱ���ж��������ռ�������Ӧ�ã�����ѧ��ת����������

��ϰ��ϵ�д�
 ��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д� Сѧ��ĩ���Ծ�ϵ�д�
Сѧ��ĩ���Ծ�ϵ�д�
�����Ŀ
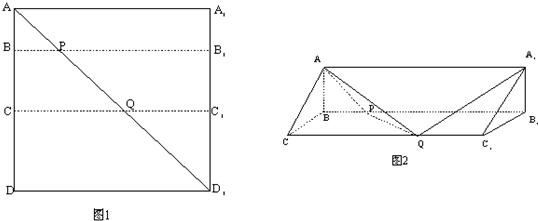
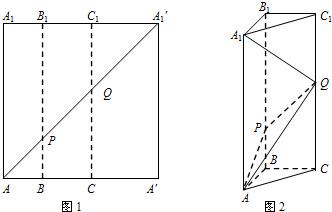 ��ͼ1��ʾ���ڱ߳�Ϊ12��������AA��A1��A1�У���B��C���߶�AA���ϣ���AB=3��BC=4����BB1��AA1���ֱ�A1A1�䡢AA1���ڵ�B1��P����CC1��AA1���ֱ�A1A1�䡢AA1���ڵ�C1��Q��������������BB1��CC1�۵���ʹ��A��A1����AA1�غϣ�������ͼ2��ʾ��������ABC-A1B1C1��
��ͼ1��ʾ���ڱ߳�Ϊ12��������AA��A1��A1�У���B��C���߶�AA���ϣ���AB=3��BC=4����BB1��AA1���ֱ�A1A1�䡢AA1���ڵ�B1��P����CC1��AA1���ֱ�A1A1�䡢AA1���ڵ�C1��Q��������������BB1��CC1�۵���ʹ��A��A1����AA1�غϣ�������ͼ2��ʾ��������ABC-A1B1C1��
 ��ͼ1��ʾ���ڱ߳�Ϊ
��ͼ1��ʾ���ڱ߳�Ϊ