题目内容
(本小题满分14分)已知数列{an}中,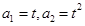 (t>0且t≠1).若
(t>0且t≠1).若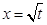 是函数
是函数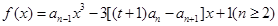 的一个极值点.
的一个极值点.
(Ⅰ)证明数列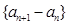 是等比数列,并求数列
是等比数列,并求数列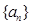 的通项公式;
的通项公式;
(Ⅱ)记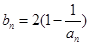 ,当t=2时,数列
,当t=2时,数列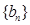 的前n项和为Sn,求使Sn>2008的n的最小值;
的前n项和为Sn,求使Sn>2008的n的最小值;
(Ⅲ)当t=2时,求证:对于任意的正整数n,有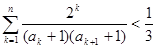 。
。
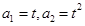 (t>0且t≠1).若
(t>0且t≠1).若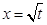 是函数
是函数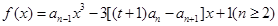 的一个极值点.
的一个极值点.(Ⅰ)证明数列
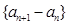 是等比数列,并求数列
是等比数列,并求数列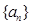 的通项公式;
的通项公式;(Ⅱ)记
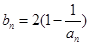 ,当t=2时,数列
,当t=2时,数列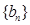 的前n项和为Sn,求使Sn>2008的n的最小值;
的前n项和为Sn,求使Sn>2008的n的最小值;(Ⅲ)当t=2时,求证:对于任意的正整数n,有
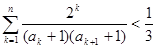 。
。解:分析:利用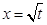 是函数
是函数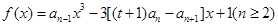 的一个极值点求出
的一个极值点求出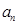 与
与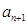 的关系式,从而加以证明第(1)问,而第(2)问的解决关键在于运用等比数列的求和公式,再利用函数的单调性得出n的最小值。第(3)问中先将
的关系式,从而加以证明第(1)问,而第(2)问的解决关键在于运用等比数列的求和公式,再利用函数的单调性得出n的最小值。第(3)问中先将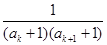 拆项并求和,通过观察与分析得出指数函数g(x)的表达式。
拆项并求和,通过观察与分析得出指数函数g(x)的表达式。
(Ⅰ)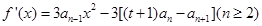 .由题意
.由题意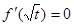 ,即
,即
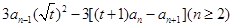 ,∴
,∴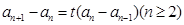 ,
,
∵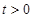 且
且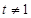 ,∴数列
,∴数列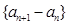 是以
是以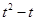 为首项,t为公比的等比数列,
为首项,t为公比的等比数列,
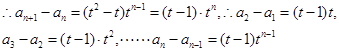
以上各式两边分别相加得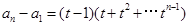 ,∴
,∴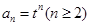 ,
,
当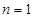 时,上式也成立,∴
时,上式也成立,∴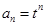
(Ⅱ)当t=2时,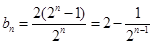
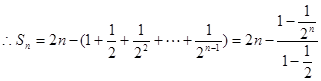
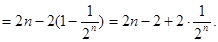
由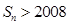 ,得
,得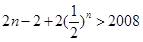 ,
,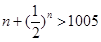 ,
,
当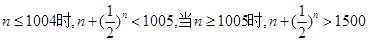 ,
,
因此n的最小值为1005.
(Ⅲ)∵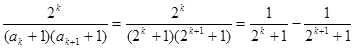
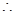
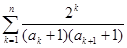
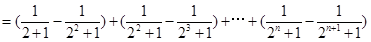
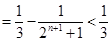
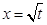 是函数
是函数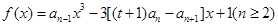 的一个极值点求出
的一个极值点求出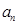 与
与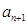 的关系式,从而加以证明第(1)问,而第(2)问的解决关键在于运用等比数列的求和公式,再利用函数的单调性得出n的最小值。第(3)问中先将
的关系式,从而加以证明第(1)问,而第(2)问的解决关键在于运用等比数列的求和公式,再利用函数的单调性得出n的最小值。第(3)问中先将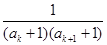 拆项并求和,通过观察与分析得出指数函数g(x)的表达式。
拆项并求和,通过观察与分析得出指数函数g(x)的表达式。(Ⅰ)
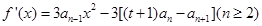 .由题意
.由题意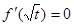 ,即
,即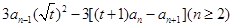 ,∴
,∴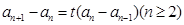 ,
,∵
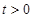 且
且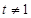 ,∴数列
,∴数列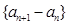 是以
是以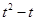 为首项,t为公比的等比数列,
为首项,t为公比的等比数列,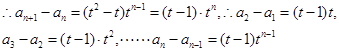
以上各式两边分别相加得
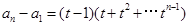 ,∴
,∴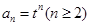 ,
,当
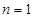 时,上式也成立,∴
时,上式也成立,∴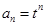
(Ⅱ)当t=2时,
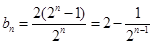
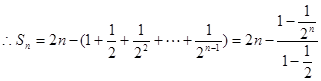
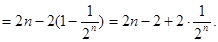
由
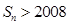 ,得
,得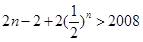 ,
,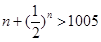 ,
,当
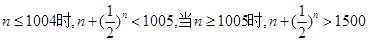 ,
,因此n的最小值为1005.
(Ⅲ)∵
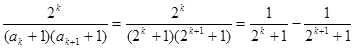
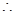
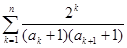
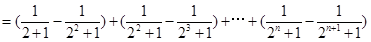
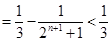
略

练习册系列答案
相关题目
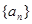 是的前n项和为Sn,满足
是的前n项和为Sn,满足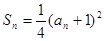
 中,
中,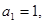 且点
且点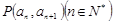 在直线
在直线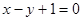 上。
上。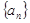 的通项公式;
的通项公式; (Ⅱ)若函数
(Ⅱ)若函数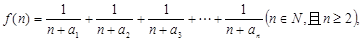 求函数
求函数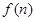 的最小值;
的最小值; (Ⅲ)设
(Ⅲ)设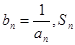 表示数列
表示数列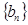 的前
的前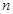 项和。试问:是否存在关于
项和。试问:是否存在关于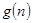 ,使得
,使得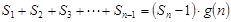 对于一切不小于2的自然数
对于一切不小于2的自然数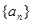 的前
的前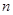 项和记为
项和记为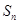 ,
,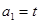 ,点
,点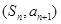 在直线
在直线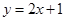 上,
上, .
. 为何值时,数列
为何值时,数列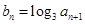 ,
,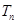 是数列
是数列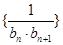 的前
的前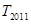 的值.
的值.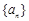 的前
的前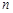 项和为
项和为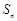 ,
,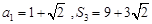
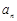 与前
与前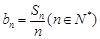 求证:数列
求证:数列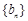 中任意不同的三项都不可能成为等比数列
中任意不同的三项都不可能成为等比数列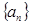 的前
的前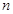 项和为
项和为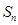 ,点
,点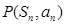 在直线
在直线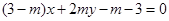 上,(
上,(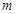 为常数,
为常数,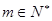 ,
,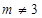 ).
).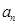 ;
;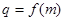 ,数列
,数列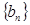 满足
满足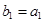 ,
,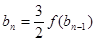 ,
,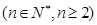 ,求证:
,求证: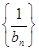 为等差数列,并求
为等差数列,并求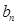 ;
;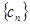 满足
满足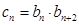 ,
,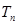 为数列
为数列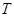 满足
满足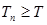
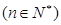 ,求
,求 为等差数列,若
为等差数列,若 ,则
,则 的值为( )
的值为( )


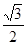
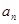 }的前n项和为
}的前n项和为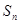 ,若
,若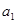 =" -11" ,
=" -11" ,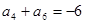 ,则当
,则当