题目内容
(本题满分16分)
已知数列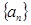 中,
中,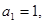 且点
且点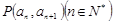 在直线
在直线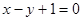 上。
上。
(Ⅰ)求数列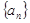 的通项公式;
的通项公式;
 (Ⅱ)若函数
(Ⅱ)若函数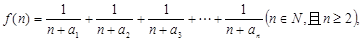 求函数
求函数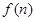 的最小值;
的最小值;
 (Ⅲ)设
(Ⅲ)设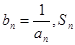 表示数列
表示数列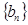 的前
的前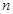 项和。试问:是否存在关于
项和。试问:是否存在关于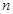 的整式
的整式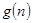 ,使得
,使得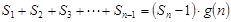 对于一切不小于2的自然数
对于一切不小于2的自然数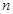 恒成立? 若存在,写出
恒成立? 若存在,写出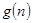 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
已知数列
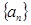 中,
中,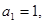 且点
且点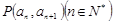 在直线
在直线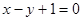 上。
上。(Ⅰ)求数列
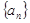 的通项公式;
的通项公式; (Ⅱ)若函数
(Ⅱ)若函数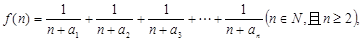 求函数
求函数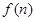 的最小值;
的最小值; (Ⅲ)设
(Ⅲ)设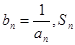 表示数列
表示数列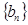 的前
的前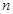 项和。试问:是否存在关于
项和。试问:是否存在关于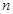 的整式
的整式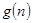 ,使得
,使得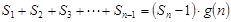 对于一切不小于2的自然数
对于一切不小于2的自然数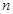 恒成立? 若存在,写出
恒成立? 若存在,写出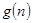 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。解:(1)由点P 在直线
在直线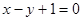 上,即
上,即 , ------------2分
, ------------2分
且 ,数列{
,数列{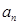 }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列
 ,
, 同样满足,所以
同样满足,所以 ---------------4分
---------------4分
(2)
 -----------6分
-----------6分

所以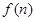 是单调递增,故
是单调递增,故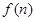 的最小值是
的最小值是 ----------------10分
----------------10分
(3) ,可得
,可得 ,
, -------12分
-------12分
 ,
,

……


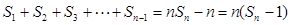 ,n≥2------------------14分
,n≥2------------------14分

故存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立----16分
 在直线
在直线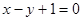 上,即
上,即 , ------------2分
, ------------2分且
 ,数列{
,数列{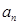 }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列 ,
, 同样满足,所以
同样满足,所以 ---------------4分
---------------4分(2)

 -----------6分
-----------6分
所以
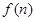 是单调递增,故
是单调递增,故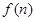 的最小值是
的最小值是 ----------------10分
----------------10分(3)
 ,可得
,可得 ,
, -------12分
-------12分 ,
,
……


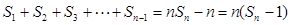 ,n≥2------------------14分
,n≥2------------------14分
故存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立----16分
略

练习册系列答案
相关题目
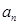 }的前n项和为Sn,若a1 =" -2" ,a2=2, 且an + 2-an=1+(-1)n 则S50 =
}的前n项和为Sn,若a1 =" -2" ,a2=2, 且an + 2-an=1+(-1)n 则S50 = 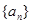 的前n项和为
的前n项和为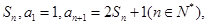 等差数列
等差数列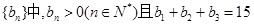 ,又
,又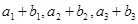 成等比数列.
成等比数列.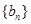 的通项公式;
的通项公式;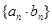 的前n项和
的前n项和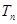 .
.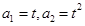 (t>0且t≠1).若
(t>0且t≠1).若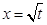 是函数
是函数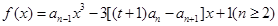 的一个极值点.
的一个极值点.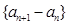 是等比数列,并求数列
是等比数列,并求数列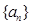 的通项公式;
的通项公式;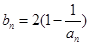 ,当t=2时,数列
,当t=2时,数列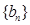 的前n项和为Sn,求使Sn>2008的n的最小值;
的前n项和为Sn,求使Sn>2008的n的最小值;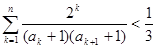 。
。 中,若
中,若 ,则
,则 的值为
的值为 满足
满足 ,则数列
,则数列 _______________.
_______________. 是等差数列,
是等差数列, ,
, ,则
,则
 满足
满足
 ,则
,则 =_________;
=_________;
 满足
满足 ,则
,则