题目内容
4.已知函数f(x)=|lnx|,g(x)=$\left\{\begin{array}{l}0,0<x≤1\\|{{x^2}-4}|-2,x>1\end{array}$,则方程|f(x)+g(x)|=1实根的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 对x分类讨论:当0<x≤1时,显然可知有一实根;
当x>1时,方程可化为|x2-4|=1-lnx或|x2-4|=3-lnx,构造函数,画出函数图象,把方程问题转换为函数交点问题,
利用数形结合思想判断即可.
解答 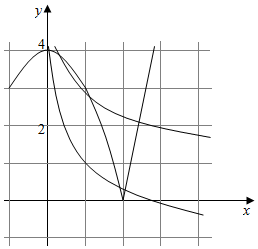 解:当0<x≤1时,
解:当0<x≤1时,
f(x)=-lnx,g(x)=0,
∴|f(x)+g(x)|=|-lnx|=1有一实根;
当x>1时,
f(x)=lnx,g(x)=|x2-4|-2,
∴|f(x)+g(x)|=|lnx+g(x)|=1,
∴|x2-4|=1-lnx或|x2-4|=3-lnx,
分别画出函数的图象如图:
,由图可知共有3个交点,
故实根的个数为4个,
故选C.
点评 本题考查了对抽象函数分类问题和利用构造函数,把方程问题转换为函数交点问题,通过数形结合思想解决实际问题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
14.已知i是虚数单位,则复数z=i(1-i)的实部为( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
15.设数列{an}的前n项和Sn=n2+n,则a4的值为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
12.程序框图如图所示,其输出S的结果是( )>


| A. | 6 | B. | 24 | C. | 120 | D. | 720 |
13.[x]表示不超过x的最大整数,则下列算法中输出的S=( )


| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
14.某程序框图如图所示,若输出S=1,则判断框中M为( )


| A. | k<3? | B. | k≤3? | C. | k≤4? | D. | k>4? |
 某学校高三年级800名学生在一次百米测试中,成绩全部介于13秒与18秒之间.抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14);第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部介于13秒与18秒之间.抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14);第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.