题目内容

已知|x-3|-|x-a|＞6有解，则实数a的取值范围
 
．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：由绝对值不等式的几何意义可知：|x-3|-|x-a|≤|a-3|，依题意得|a-3|＞6，解之即可．
解答： 解：∵|x-3|-|x-a|≤|a-3|，
∴|x-3|-|x-a|＞6有解?|a-3|＞6，解得：a＜-3或a＞9，
即实数a的取值范围为（-∞，-3）∪（9，+∞），
故答案为：（-∞，-3）∪（9，+∞）．
点评：本题主要考查绝对值不等式的解法，着重考查绝对值的意义，考查转化思想．
练习册系列答案
相关题目
已知a=20.8，b=20.3，c=ln
1
2
，则a，b，c三者由小到大的顺序为
 
．
计算：
（1）81
1
2
+(-7)0-(
1
3
)-2；
（2）log464+lg25+lg4+9log92．
y=sin（-2x+
π
3
）经过怎样变换得到y=sin2x的图象．
若α∈[0，2π]，用
1+cosα
2
+
1-cosα
2
=sin
α
2
-cos
α
2
．则α的取值范围是
 
．
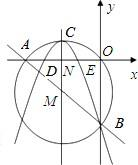如图所示，在平面直角坐标系中，圆M经过原点O且与x轴y轴分别相交于A（-6，0），B（0，-8）两点，若有一抛物线的对称轴平行于y轴且经过点M，顶点C在圆M上，开口向下，且经过B．
（1）求此抛物线的函数解析式，且设抛物线交x轴于D、E两点，在抛物线上是否存在点P，使得S△PDE=
1
10
S△ABC，若存在，请求出点P的坐标；
（2）在抛物线上找点F使∠AFB为锐角，直接写出F的横坐标范围；
（3）求出△ABO内切圆的圆心坐标；
（4）求圆心在抛物线的对称轴上，且与直线AB和x轴都相切的圆的半径是多少？
（5）求过C、D、E三点外接圆的半径．
已知装曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)的渐近线过点(1，
3
)，F1，F2为双曲线的左右焦点，P为双曲线上的任意一点，且∠F1PF2=
π
3
，S△PF1F2=12
3
．
（1）求双曲线的两条渐近线的夹角；
（2）求双曲线的标准方程．
如图，三棱锥P-ABC，底面ABC为边长为2
3
的正三角形，平面PBC⊥平面ABC，PB=PC=2，D为AP上一点，AD=2DP，O为底面三角形中心．
（1）求证：DO∥面PBC；
（2）求证：AC⊥面BOD；
（3）设M为PC中点，求二面角M-BD-O的余弦值．
△ABC与A1、B1、C1不在同一平面内，如果三条直线AA1，BB1，CC1，两两相交，求证：AA1，BB1，CC1交于一点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网