题目内容
15.已知:a、b、c∈R+,a+b+c=1,求a2+b2+c2的最小值.分析 利用3(a2+b2+c2)≥(a+b+c)2即可得出.
解答 解:∵(a-b)2+(b-c)2+(a-c)2≥0,
化为2(a2+b2+c2)≥2ab+2ac+2bc,
∴3(a2+b2+c2)≥(a+b+c)2=1,
可得a2+b2+c2≥$\frac{1}{3}$,当且仅当a=b=c=$\frac{1}{3}$时取等号.
∴a2+b2+c2的最小值为$\frac{1}{3}$.
点评 本题考查了基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.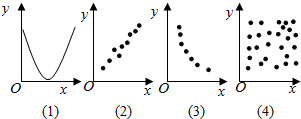 如图,两个变量具有相关关系的图是( )
如图,两个变量具有相关关系的图是( )
 如图,两个变量具有相关关系的图是( )
如图,两个变量具有相关关系的图是( )| A. | (1)(2) | B. | (1)(3) | C. | (2)(4) | D. | (2)(3) |
7.函数$f(x)=\frac{x^2}{{\sqrt{2-x}}}+lg(x+3)$的定义域为( )
| A. | (-3,2] | B. | [-3,2] | C. | (-3,2) | D. | (-∞,-3) |
4.点$(\sqrt{2},\sqrt{3})$在双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)上,且C的焦距为4,则它的离心率为( )
| A. | 2 | B. | 4 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
5.已知集合S={y|y=2x},T={x|y=lg(x+1)},则S∩T=( )
| A. | (0,+∞) | B. | [0,+∞) | C. | (-1,+∞) | D. | [-1,+∞) |