题目内容
已知:椭圆C: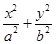 =1(a>b>0)的左、右焦点为F1、F2,e=
=1(a>b>0)的左、右焦点为F1、F2,e=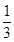 ,过F1的直线l交椭圆C于A、B两点,|AF2|、|AB|、|BF2|成等差数列,且|AB|=4。
,过F1的直线l交椭圆C于A、B两点,|AF2|、|AB|、|BF2|成等差数列,且|AB|=4。
(I)求椭圆C的方程;
(II)M、N是椭画C上的两点,若线段MN被直线x=1平分,证明:线段MN的中垂线过定点。
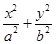 =1(a>b>0)的左、右焦点为F1、F2,e=
=1(a>b>0)的左、右焦点为F1、F2,e=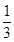 ,过F1的直线l交椭圆C于A、B两点,|AF2|、|AB|、|BF2|成等差数列,且|AB|=4。
,过F1的直线l交椭圆C于A、B两点,|AF2|、|AB|、|BF2|成等差数列,且|AB|=4。(I)求椭圆C的方程;
(II)M、N是椭画C上的两点,若线段MN被直线x=1平分,证明:线段MN的中垂线过定点。
解:(Ⅰ)∵
 、
、 、
、 成等差数列,
成等差数列,∴
 . ………2分
. ………2分∴
 ,……5分
,……5分得
 ,又
,又 ,所以
,所以 ,
, ,
,所求的椭圆方程为:
 . ………7分
. ………7分(Ⅱ)设
 ,
, ,
,由题意知:
 ,
, . ………9分
. ………9分两式相减得:
 ,
,∴
 ,
,所以

 , ………11分
, ………11分易证,此直线经过定点
 . ………13分
. ………13分略

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 ,数列
,数列 的首项
的首项
 ,数列
,数列 的前n项和为
的前n项和为 ,求使
,求使 的最小正整数n。
的最小正整数n。 及两点
及两点 和
和 ,其中
,其中 .过
.过 ,
, 分别作
分别作 轴的垂线,交抛物线于
轴的垂线,交抛物线于 ,
, 两点,直线
两点,直线 与
与 ,此时就称
,此时就称 .依此类推,可由
.依此类推,可由 ,
, .记
.记 ,
, .
. 是递减数列;
是递减数列; ,
, ;
; ,
, ,则
,则 .
.
 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且 ,
, 。
。 求数列
求数列 的前n项和Sn。
的前n项和Sn。 的前项和为
的前项和为 ,
, 且
且 ,则使得
,则使得 中,首项
中,首项 公差
公差 ,若
,若 ,则
,则 ( )
( )



 满足
满足 ……+
……+ ,则有 ( )
,则有 ( )



 ,
,