题目内容
 如图,⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.
如图,⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.(1)求证:圆心O在直线AD上;
(2)若BC=2,求GC的长.
考点:与圆有关的比例线段
专题:立体几何
分析:(I)由已知条件得CF=BE,CD=BD,由△ABC是等腰三角形,得AD是∠CAB的平分线,由此能证明圆心O在直线AD上.
(II)连接DF,由已知条件得∠FDH+FHD=90°,∠G=∠FDH,由此能求出GC的长.
(II)连接DF,由已知条件得∠FDH+FHD=90°,∠G=∠FDH,由此能求出GC的长.
解答:
 (I)证明:∵AB=AC,AF=AE
(I)证明:∵AB=AC,AF=AE
∴CF=BE…(2分)
又CF=CD,BD=BE,∴CD=BD…(4分)
又△ABC是等腰三角形
∴AD是∠CAB的平分线
∴圆心O在直线AD上…(6分)
(II)解:连接DF,由(I)知,DH是⊙O的直径
∴∠DFH=90°,∴∠FDH+FHD=90°…(7分)
又∠G+∠FHD=90°,∴∠G=∠FDH…(8分)
∵⊙O与AC相切于点F,∴∠AFH=∠GFC=∠FDH
∴∠GFC=∠G…(10分)
∴CG=CF=CD=DB
由BC=2,得GC=1.…(12分)
 (I)证明:∵AB=AC,AF=AE
(I)证明:∵AB=AC,AF=AE∴CF=BE…(2分)
又CF=CD,BD=BE,∴CD=BD…(4分)
又△ABC是等腰三角形
∴AD是∠CAB的平分线
∴圆心O在直线AD上…(6分)
(II)解:连接DF,由(I)知,DH是⊙O的直径
∴∠DFH=90°,∴∠FDH+FHD=90°…(7分)
又∠G+∠FHD=90°,∴∠G=∠FDH…(8分)
∵⊙O与AC相切于点F,∴∠AFH=∠GFC=∠FDH
∴∠GFC=∠G…(10分)
∴CG=CF=CD=DB
由BC=2,得GC=1.…(12分)
点评:本题考查圆心在直线上的证明,考查线线段长的求法,解题时要认真审题,注意圆的简单性质的合理运用.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
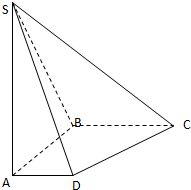 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=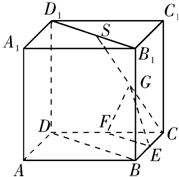 如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证:
如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证: 如图是某算法的程序框图,若任意输入[
如图是某算法的程序框图,若任意输入[