题目内容
已知数列{xn}满足x1=
,且xn+1=
,(n∈N+)
(1)用数学归纳证明:0<xn<1
(2)设an=
,求数列{an}的通项公式.
| 1 |
| 2 |
| xn |
| 2-xn |
(1)用数学归纳证明:0<xn<1
(2)设an=
| 1 |
| xn |
考点:数学归纳法
专题:点列、递归数列与数学归纳法
分析:(1)根据数学归纳法的证明步骤进行证明;
(2)设an=
,可得{an-1}是以1为首项,以2为公比的等比数列,即可求数列{an}的通项公式.
(2)设an=
| 1 |
| xn |
解答:
(1)证明:①当n=1时,x1=
∈(0,1),
②假设当n=k时,结论成立,即xk∈(0,1),
则当n=k+1时,xk+1=f(xk)=
∵xk∈(0,1),
∴
∈(0,1),
即n=k+1时结论成立
综上①②可知0<xn<1;…(6分)
(2)解:由xn+1=
可得:
=
-1
∵an=
,
∴an+1=2an-1,
∴an+1-1=2(an-1)…(8分)
又a1-1=1
∴{an-1}是以1为首项,以2为公比的等比数列,
∴an-1=2n-1,
即an=2n-1+1…(12分)
| 1 |
| 2 |
②假设当n=k时,结论成立,即xk∈(0,1),
则当n=k+1时,xk+1=f(xk)=
| xk |
| 2-xk |
∵xk∈(0,1),
∴
| xk |
| 2-xk |
即n=k+1时结论成立
综上①②可知0<xn<1;…(6分)
(2)解:由xn+1=
| xn |
| 2-xn |
| 1 |
| xn+1 |
| 2 |
| xn |
∵an=
| 1 |
| xn |
∴an+1=2an-1,
∴an+1-1=2(an-1)…(8分)
又a1-1=1
∴{an-1}是以1为首项,以2为公比的等比数列,
∴an-1=2n-1,
即an=2n-1+1…(12分)
点评:本题考查根据递推关系求数列的通项公式的方法,考查数学归纳法,证明n=k+1时,是解题的难点.

练习册系列答案
相关题目
已知向量
,
满足|
|=5,|
|=4,|
-
|=
,则
与
的夹角θ=( )
| a |
| b |
| a |
| b |
| b |
| a |
| 61 |
| a |
| b |
| A、150° | B、120° |
| C、60° | D、30° |
 某学习小组共9人,在如图所示的方格中选择一个座位,根据以往的学习经验,学习互助伙伴越多,学习成绩越好(互助伙伴指两个学生座位是前后或左右关系且相邻),每个学生期末成
某学习小组共9人,在如图所示的方格中选择一个座位,根据以往的学习经验,学习互助伙伴越多,学习成绩越好(互助伙伴指两个学生座位是前后或左右关系且相邻),每个学生期末成 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=AD=2.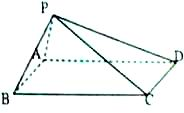 如图,四棱锥P-ABCD的底面ABCD是矩形,且AB=2,BC=
如图,四棱锥P-ABCD的底面ABCD是矩形,且AB=2,BC=