题目内容
如图,函数f(x)=x+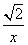 的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.
的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.
(1)证明:|PM|·|PN|为定值;
(2)O为坐标原点,求四边形OMPN面积的最小值.
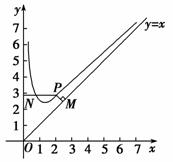
(1)证明:设P(x0,x0+ )(x0>0),则|PN|=x0,|PM|=
)(x0>0),则|PN|=x0,|PM|= =
= ,因此|PM|·|PN|=1.
,因此|PM|·|PN|=1.
(2)直线PM的方程为y-x0- =-(x-x0),
=-(x-x0),
即y=-x+2x0+ ,解方程组
,解方程组
得x=y=x0+ ,∴M(x0+
,∴M(x0+ ,x0+
,x0+ ).连接OP,
).连接OP,
S四边形OMPN=S△NPO+S△OPM=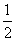 |PN||ON|+
|PN||ON|+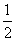 |PM||OM|=
|PM||OM|=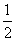 x0(x0+
x0(x0+ )+
)+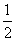 ·
· ·
· (x0+
(x0+ )=
)= +
+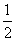 (x
(x +
+ )≥1+
)≥1+ ,
,
当且仅当x =
= ,即x0=1时等号成立,因此四边形OMPN面积的最小值为1+
,即x0=1时等号成立,因此四边形OMPN面积的最小值为1+ .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 (x>1)的最小值是( )
(x>1)的最小值是( ) +2 B.2
+2 B.2 则目标函数z=4x+y的最大值为________.
则目标函数z=4x+y的最大值为________.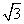 ,将直线绕点P顺时针旋转60°所得的直线l的斜率是( )
,将直线绕点P顺时针旋转60°所得的直线l的斜率是( )
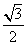

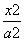 +
+ =1(a>b>0)的左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若
=1(a>b>0)的左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )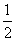 B.
B.
 D.
D.