题目内容
各项均为正数的数列 对一切
对一切 均满足
均满足 .证明:
.证明:
(1) ;
;
(2) .
.
(1)详见解析,(2)详见解析.
解析试题分析:(1)作差证明不等式,因为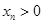 ,
, ,所以
,所以 ,且
,且 .
.
因此 .即
.即 .(2)本题证明:
.(2)本题证明: 用数学归纳法,而证明
用数学归纳法,而证明 用反证法. ① 当
用反证法. ① 当 时,由题设
时,由题设 可知
可知 成立;② 假设
成立;② 假设 时,
时, ,
,
当 时,由(1)得,
时,由(1)得, .由①,②可得,
.由①,②可得, .假设存在自然数
.假设存在自然数 ,使得
,使得 ,则一定存在自然数
,则一定存在自然数 ,使得
,使得 .因为
.因为 ,
, ,
, , ,
, ,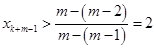 ,与题设
,与题设 矛盾,所以,
矛盾,所以, .若
.若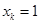 ,则
,则 ,根据上述证明可知存在矛盾.
,根据上述证明可知存在矛盾.
【证明】(1)因为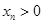 ,
, ,与题设
,与题设 矛盾,所以,
矛盾,所以, .若
.若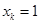 ,则
,则 ,根据上述证明可知存在矛盾.
,根据上述证明可知存在矛盾.
所以 ,
,
所以 ,且
,且 .
.
因为 .
.
所以 ,
,
所以 ,即
,即 . 4分
. 4分
(注:用反证法证明参照给分)
(2)下面用数学归纳法证明: .
.
① 当 时,由题设
时,由题设 可知结论成立;
可知结论成立;
② 假设 时,
时, ,
,
当 时,由(1)得,
时,由(1)得, .
.
由①,②可得, . 7分
. 7分
下面先证明 .
.
假设存在自然数 ,使得
,使得 ,则一定存在自然数
,则一定存在自然数 ,使得
,使得 .
.
因为 ,
, ,
, , ,
, ,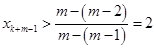 ,
,
与题设 矛盾,所以,
矛盾,所以, .
.
若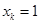 ,则
,则 ,根据上述证明可知存在矛盾.
,根据上述证明可知存在矛盾.
所以 成立. 10分
成立. 10分
考点:数学归纳法

练习册系列答案
相关题目
 时,
时,
 不可能是同一个等差数列中的三项
不可能是同一个等差数列中的三项 +
+ +…+
+…+ >
> 对一切正整数n都成立,猜想正整数a的最大值,并证明结论.
对一切正整数n都成立,猜想正整数a的最大值,并证明结论. 中,
中, ,且
,且 成等差数列,
成等差数列, 成等比数列
成等比数列 .
. ;
; ;
; 均为实数,且
均为实数,且 ,
, ,
,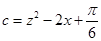 ,求证
,求证 ;
; ,试用分析法证明:
,试用分析法证明: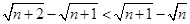 .
. 是等差数列,
是等差数列, 设
设 N+),
N+), N+),问Pn与Qn哪一个大?并证明你的结论.
N+),问Pn与Qn哪一个大?并证明你的结论.
 个等式为 ▲
个等式为 ▲