题目内容
（1）用反证法证明：在一个三角形中，至少有一个内角大于或等于
；
（2）已知
，试用分析法证明：
.
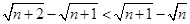（1）证明详见解析；（2）证明详见解析.
解析试题分析：（1）根据应用反证法证明命题的一般步骤，先假设原命题的结论不成立，由此找出矛盾（本题中的矛盾指向：三角形的内角和定理），从而肯定结论进行证明即可；（2）根据分析法的思路是执果索因，要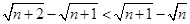证，只需证
，进而结合不等式的性质：不等式的可乘方性，进行逐渐整理即可得到最后只须证
，显然成立，从而命题得证.
试题解析：（1）证明：假设在一个三角形中，没有一个内角大于或等于，即均小于
则三内角和小于
，与三角形中三内角和等于矛盾，故假设不成立，原命题成立；
（2）证明：要证上式成立，需证
需证
需证
需证
需证
只需证
因为显然成立，所以原命题成立.
考点：1.反证法；2.分析法.
练习册系列答案
相关题目
(a>1)．
对一切
均满足
．证明：
；
．
(
)
均为实数，且
，
，
求证：
满足：集合
中至少存在三个不同的数构成等比数列，则称函数
；②
中，哪些是等比源函数？（不需证明）
，函数
不是等比源函数；
，函数
都是等比源函数.
(a＞1)．
，
＋
＋ ＋
(n∈N*)．
中，若
，则有等式
（
，
）成立．类比上述性质，相应地，在等比数列
中，若
，则有等式 成立．