题目内容
5．四面体ABCD中，AB=2，BC=3，CD=4，DB=5，AC=$\sqrt{13}$，AD=$\sqrt{29}$，则四面体ABCD外接球的表面积是29π．分析 由题意，DC⊥AC，DC⊥BC，AB⊥BC，将四面体扩充为长方体，体对角线长为$\sqrt{16+13}$=$\sqrt{29}$，即可求出四面体ABCD外接球的表面积．
解答 解：由题意，DC⊥AC，DC⊥BC，AB⊥BC，
将四面体扩充为长方体，体对角线长为$\sqrt{16+13}$=$\sqrt{29}$，
∴四面体ABCD外接球的表面积是$4π•（\frac{\sqrt{29}}{2}）^{2}$=29π．
故答案为29π．
点评 本题考查四面体ABCD外接球的表面积，将四面体扩充为长方体，求出体对角线长是关键．
练习册系列答案
备战中考寒假系列答案
相关题目
15．2016年1月1日起全国统一实施全面两孩政策，为了解适龄民众对放开生育二胎政策的态度，某市选取70后和80后作为调查对象，随机调查了100位，得到数据如表：
根据以上调查数据，认为“生二胎与年龄有关”的把握有（ ）
参考公式：x2=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1}•{n}_{2}•n•1•n•2}$，其中n=n11+n12+n21+n22．
参考数据：
| 生二胎 | 不生二胎 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
参考公式：x2=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1}•{n}_{2}•n•1•n•2}$，其中n=n11+n12+n21+n22．
参考数据：
| P（x2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
| A． | 90% | B． | 95% | C． | 99% | D． | 99.9% |
如图，在三棱柱ABC-A1B1C1中，CA=CB=AA1，∠BAA1=∠BAC=60°，点O是线段AB的中点．
20．在两坐标轴上截距均为m（m∈R）的直线l1与直线l2：2x+2y-3=0的距离为$\sqrt{2}$，则m=（ ）
| A． | $\frac{7}{2}$ | B． | 7 | C． | -1或7 | D． | -$\frac{1}{2}$或$\frac{7}{2}$ |
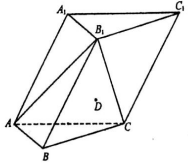如图，在各棱长均为2的三棱柱ABC-A1B1C1中，侧面A1ACC1⊥底面ABC，∠A1AC=60°．