题目内容
已知函数 的定义域为
的定义域为 ,部分对应值如下表,
,部分对应值如下表,
 的导函数
的导函数 的图象如图所示. 下列关于
的图象如图所示. 下列关于 的命题:
的命题:
①函数 的极大值点为
的极大值点为 ,
, ;
;
②函数 在
在 上是减函数;
上是减函数;
③如果当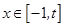 时,
时, 的最大值是2,
的最大值是2,
那么 的最大值为4;
的最大值为4;
④当 时,函数
时,函数 有
有 个零点;
个零点;
⑤函数 的零点个数可能为0、1、2、3、4个.其中正确命题的个数是
的零点个数可能为0、1、2、3、4个.其中正确命题的个数是
| A.4 | B.3 | C.2 | D.1 |
B
解析试题分析:根据题意,根据函数 的定义域为
的定义域为 ,以及部分的对应值如下表,
,以及部分的对应值如下表, ,
,
导数图象说明原函数增减增减的变化趋势,可知在x=0取得极大值x=2处取得极小值,在x=4处取得极大值,故①函数 的极大值点为
的极大值点为 ,
, ;正确
;正确
对于②函数 在
在 上是减函数;也成立,对于③如果当
上是减函数;也成立,对于③如果当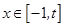 时,
时, 的最大值是2,
的最大值是2,
那么 的最大值为4;错误对于④当
的最大值为4;错误对于④当 时,函数
时,函数 有
有 个零点;错误。
个零点;错误。
⑤函数 的零点个数可能为0、1、2、3、4个,成立。故正确的命题有3个,选B.
的零点个数可能为0、1、2、3、4个,成立。故正确的命题有3个,选B.
考点:函数与导函数
点评:主要是考查了导数研究函数单调性以及极值的运用就,属于中档题。

练习册系列答案
相关题目
函数f(x)=2x2-mx+2当x∈[-2,+∞)时是增函数,则m的取值范围是( )
| A.(-∞,+∞) | B.[8,+∞) | C.(-∞,-8] | D.(-∞,8] |
函数 的图象如图所示,则
的图象如图所示,则 的解析式可能是 ( )
的解析式可能是 ( ) 
A. | B. |
C. | D. |
定义在 上的偶函数
上的偶函数 满足:对任意
满足:对任意 、
、
 (
(

 ),有
),有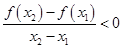 ,则( )
,则( )
A. |
B. |
C. |
D. |
已知 是定义在R上的奇函数,若对于x≥0,都有f(x+2)=
是定义在R上的奇函数,若对于x≥0,都有f(x+2)= ,且
,且
当 时,
时, ,则
,则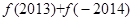 =( )
=( )
| A.1-e | B.e-1 | C.-l-e | D.e+l |
已知f(x)是奇函数,g(x)是偶函数,且f(-1)+g(1)=2,f(1)+g(-1)=4,则g(1)等于( )
| A.4 | B.3 | C.2 | D.1 |
 和
和 ,动点
,动点 在直线
在直线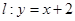 上移动,椭圆
上移动,椭圆 以
以 为焦点且经过点
为焦点且经过点 ,记椭圆
,记椭圆 ,则函数
,则函数 的大致图像( )
的大致图像( )
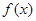 (
( R)满足
R)满足 ,
, ,则函数
,则函数 的图像是( )
的图像是( ) 





