题目内容
函数f(x)=2x2-mx+2当x∈[-2,+∞)时是增函数,则m的取值范围是( )
| A.(-∞,+∞) | B.[8,+∞) | C.(-∞,-8] | D.(-∞,8] |
C
解析试题分析:函数f(x)=2x2-mx+2的对称轴是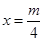 ,由于函数f(x)在[-2,+∞)上是增函数,则
,由于函数f(x)在[-2,+∞)上是增函数,则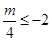 ,解得
,解得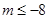 ,则m的取值范围是(-∞,-8]。故选C。
,则m的取值范围是(-∞,-8]。故选C。
考点:函数的单调性
点评:本题的函数是二次函数,其对称轴两边的单调性不一致,由于此函数的开口向上,故对称轴左边为减函数,右边为增函数。

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
函数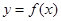 的图像如图所示,在区间
的图像如图所示,在区间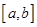 上可找到
上可找到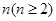 个不同的数
个不同的数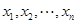 ,使得
,使得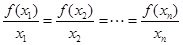 ,则
,则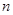 的取值范围为( )
的取值范围为( )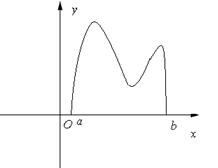
A.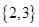 | B.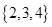 |
C.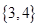 | D. |
已知函数f(x)="a" sinx-bcosx (a、b为常数,a≠0,x∈R)在x=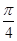 处取得最小值,则函数y=f(
处取得最小值,则函数y=f(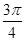 -x)是( )
-x)是( )
| A.偶函数且它的图象关于点(π,0)对称 |
B.偶函数且它的图象关于点(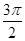 ,0)对称 ,0)对称 |
C.奇函数且它的图象关于点(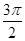 ,0)对称 ,0)对称 |
| D.奇函数且它的图象关于点(π,0)对称 |
若定义运算: ,例如
,例如 ,则下列等式不能成立的是( )
,则下列等式不能成立的是( )
A. | B. |
C. | D. ( ( ) ) |
若函数 有极值点
有极值点 ,且
,且 ,则关于
,则关于 的方程
的方程 的不同实根个数是( )
的不同实根个数是( )
| A.3 | B.4 |
| C.5 | D.6 |
 ,如果存在区间
,如果存在区间 ,同时满足下列条件:
,同时满足下列条件: 在
在 存在“和谐区间”,则
存在“和谐区间”,则 的取值范围是( )
的取值范围是( )
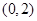
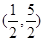

 (万元)与时间
(万元)与时间 (天)的关系如图所示,已知该公司在该年度中每天平均利润为35万元,令
(天)的关系如图所示,已知该公司在该年度中每天平均利润为35万元,令 (万元)表示时间段
(万元)表示时间段 内该公司的平均利润,则
内该公司的平均利润,则
 的定义域为
的定义域为 ,部分对应值如下表,
,部分对应值如下表,
 的图象如图所示. 下列关于
的图象如图所示. 下列关于
 ,
, ;
; 上是减函数;
上是减函数;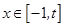 时,
时, 的最大值为4;
的最大值为4; 时,函数
时,函数 有
有 (a>0且a≠1)与函数y=(1-a)x的图象只能是( )
(a>0且a≠1)与函数y=(1-a)x的图象只能是( )