Question

【题目】在正方体ABCD﹣A1B1C1D1中：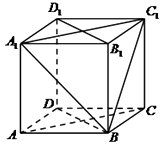
（Ⅰ）求证：AC∥平面A1BC1；
（Ⅱ）求证：平面A1BC1⊥平面BB1D1D．

Answer 1

【答案】证明：（Ⅰ）因为AA1∥CC1，所以四边形ACC1A1为平行四边形，

所以AC∥A1C1，又A1C1平面A1BC1，AC平面A1BC1，AC∥平面A1BC1；

（Ⅱ）易知A1C1⊥B1D1，因为BB1⊥平面A1B1C1D1，所以BB1⊥A1C1，

因为BB1∩B1D1=B1，所以A1C1⊥平面BB1D1D，

因为A1C1平面A1BC1，所以平面A1BC1⊥平面BB1D1D

【解析】（Ⅰ）证明四边形ACC1A1为平行四边形，可得AC∥A1C1，即可证明AC∥平面A1BC1；（Ⅱ）证明A1C1⊥平面BB1D1D，即可证明平面A1BC1⊥平面BB1D1D．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行，以及对平面与平面垂直的判定的理解，了解一个平面过另一个平面的垂线，则这两个平面垂直．