题目内容
如图,PA,PB切⊙O于A,B两点,BC∥PA交⊙O于C,MC∥AB交⊙O于D,交PB,PA的延长线于M,Q.
(1)求证:AD∥PM
(2)设⊙O的半径长为1,PA=PB=2,求CD的长

(1)求证:AD∥PM
(2)设⊙O的半径长为1,PA=PB=2,求CD的长

(1)见解析
(2)
(2)

(1)∵PA,PB切⊙O于A,B两点,
∴∠PBA=∠PAB
又BC∥PA
∴∠PAB=∠ABC
又∠ADC=∠ABC(同弧所对的圆周角相等)
∴∠PBA=∠ADC
又AB∥MC
∴∠PBA=∠M
∴∠ADC=∠M
∴AD∥PM
(2) 连接OP,OB,则OB⊥PB
∵OB=1,PB=2
∴OP=
∴AB=

连接AC
∵BC∥PQ
∴AC=AB= ,∠CAQ=∠BAP
,∠CAQ=∠BAP
又AB∥CQ
∴∠Q=∠BAP,∴∠Q=∠CAQ,即CQ=CA=
显然△PAB∽△CAQ
∴
 AQ=
AQ=
由切割线定理得
AQ2=QC·QD (
( )2=
)2= ×QD
×QD QD=
QD= =
= ×
× <QC
<QC
∴CD=QC-QD= -
- ×
× =
= ×
× =
= (此时D点在AC弧上)
(此时D点在AC弧上)
∴∠PBA=∠PAB
又BC∥PA
∴∠PAB=∠ABC
又∠ADC=∠ABC(同弧所对的圆周角相等)
∴∠PBA=∠ADC
又AB∥MC
∴∠PBA=∠M
∴∠ADC=∠M
∴AD∥PM
(2) 连接OP,OB,则OB⊥PB
∵OB=1,PB=2
∴OP=

∴AB=


连接AC
∵BC∥PQ
∴AC=AB=
 ,∠CAQ=∠BAP
,∠CAQ=∠BAP又AB∥CQ
∴∠Q=∠BAP,∴∠Q=∠CAQ,即CQ=CA=

显然△PAB∽△CAQ
∴

 AQ=
AQ=
由切割线定理得
AQ2=QC·QD
 (
( )2=
)2= ×QD
×QD QD=
QD= =
= ×
× <QC
<QC∴CD=QC-QD=
 -
- ×
× =
= ×
× =
= (此时D点在AC弧上)
(此时D点在AC弧上)
练习册系列答案
相关题目
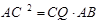
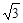 ,BP=2,求QD.
,BP=2,求QD.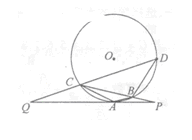
 ,则
,则 的取值范围是 .
的取值范围是 . 与圆
与圆 相切于
相切于 ,直线
,直线 交圆
交圆 ,
, 两点,
两点, ,垂足为
,垂足为 ,且
,且 的中点,若
的中点,若 ,则
,则 .
.
 中,弦
中,弦 ,
, 为
为 作
作 的延长线于点
的延长线于点 ,
, .则
.则 ____ .
____ . 
 CD.则PD=________.
CD.则PD=________.