题目内容
如图所示,矩形ABCD中,E是BC上的点,AE⊥DE,BE=4,EC=1,则AB的长为________.
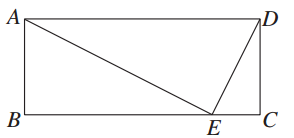

2
法一:∵∠B=90°,
∴∠BAE+∠AEB=90°.
∵AE⊥DE,
∴∠AEB+∠CED=90°.
∴∠BAE=∠CED,
∴Rt△ABE∽Rt△ECD,
∴ =
= ,即
,即 =
= ,∴AB=2.
,∴AB=2.
法二:过E作EF⊥AD于F.

由题知AF=BE=4,
DF=CE=1.
则EF2=AF·DF=4.
∴AB=EF=2.
∴∠BAE+∠AEB=90°.
∵AE⊥DE,
∴∠AEB+∠CED=90°.
∴∠BAE=∠CED,
∴Rt△ABE∽Rt△ECD,
∴
 =
= ,即
,即 =
= ,∴AB=2.
,∴AB=2.法二:过E作EF⊥AD于F.

由题知AF=BE=4,
DF=CE=1.
则EF2=AF·DF=4.
∴AB=EF=2.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目


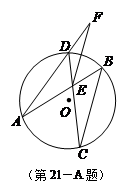
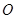 的两弦
的两弦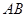 和
和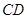 交于点
交于点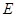 ,
,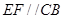 ,
,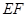 交
交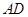 的延长线于点
的延长线于点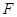 .求证:△
.求证:△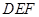 ∽△
∽△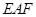 .
.
 是圆的内接三角形,
是圆的内接三角形, 的平分线交圆于点
的平分线交圆于点 ,交
,交 于点
于点 ,过点
,过点 的圆的切线与
的圆的切线与 的延长线交于点
的延长线交于点 .在上述条件下,给出下列四个结论:
.在上述条件下,给出下列四个结论:


 b
b b
b
 ,则线段CD的长为________.
,则线段CD的长为________.