题目内容
定义在R上的函数f（x）满足f（-x）+f（x）且周期是4，若f（1）=5，则f（2015）（ ）
| A、5 | B、-5 | C、0 | D、3 |
考点：函数的周期性,函数的值
专题：函数的性质及应用
分析：首先根据函数的关系式求出函数是奇函数，进一步利用函数的周期求出函数的值．
解答：
解：在R上的函数f（x）满足f（-x）+f（x）=0
则：f（-x）=-f（x）
所以函数是奇函数
由于函数周期是4，
所以f（2015）=f（504×4-1）=f（-1）=-f（1）=-5
故选：B
则：f（-x）=-f（x）
所以函数是奇函数
由于函数周期是4，
所以f（2015）=f（504×4-1）=f（-1）=-f（1）=-5
故选：B
点评：本题考查的知识要点：函数的奇偶性的应用和周期性的应用，属于基础题型．
练习册系列答案
阅读快车系列答案
相关题目
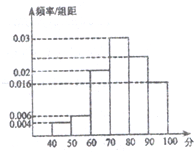从某校高三学生中抽取n名学生参加数学竞赛，根据成绩（单位：分）的分组及各数据绘制的频率分布直方图如图所示，已知成绩的范围是区间[40，100），且成绩在区间[70，90）的学生人数是27人．长方体ABCD-A1B1C1D1中，已知二面角A1-BD-A的大小为
，若空间有一条直线l与直线CC1，所成的角为
，则直线l与平面A1BD所成角的取值范围是（ ）
| π |
| 6 |
| π |
| 4 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[0，
|