题目内容
长方体ABCD-A1B1C1D1中,已知二面角A1-BD-A的大小为
,若空间有一条直线l与直线CC1,所成的角为
,则直线l与平面A1BD所成角的取值范围是( )
| π |
| 6 |
| π |
| 4 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[0,
|
考点:直线与平面所成的角
专题:空间位置关系与距离
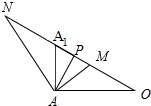
分析:如图所示,过点A作AO⊥BD,连接A1O,由三垂线定理可得BD⊥A1O,则∠AOA1为二面角A1-BD-A的平面角.把直线l平移到AM,则∠A1AM=∠MAO=
.过点A作AP⊥A1O,则AP⊥平面A1BD.利用线面角的定义可得:AM(即直线l)与平面A1BD所成的最大角为∠AMA1.假设∠A1AN=
,AN与直线OP相交于点N,则AN(即直线l)与平面A1BD所成的最小角为∠ANP.
| π |
| 4 |
| π |
| 4 |
解答:
解:如图所示,过点A作AO⊥BD,连接A1O,由三垂线定理可得BD⊥A1O,则∠AOA1为二面角A1-BD-A的平面角,∴∠AOA1=
.
把直线l平移到AM,则∠A1AM=∠MAO=
.
过点A作AP⊥A1O,则AP⊥平面A1BD.
∴AM(即直线l)与平面A1BD所成的最大角为∠AMA1=∠MAO+∠MOA=
+
=
.
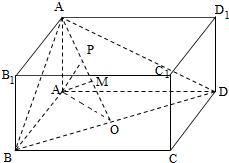
假设∠A1AN=
,AN与直线OP相交于点N,则AN(即直线l)与平面A1BD所成的最小角为
∠ANP=∠PA1A-∠A1AN=
-
=
.
∴直线l与平面A1BD所成角的取值范围是[
,
].
故选:C.
| π |
| 6 |
把直线l平移到AM,则∠A1AM=∠MAO=
| π |
| 4 |
过点A作AP⊥A1O,则AP⊥平面A1BD.
∴AM(即直线l)与平面A1BD所成的最大角为∠AMA1=∠MAO+∠MOA=
| π |
| 4 |
| π |
| 6 |
| 5π |
| 12 |


假设∠A1AN=
| π |
| 4 |
∠ANP=∠PA1A-∠A1AN=
| π |
| 3 |
| π |
| 4 |
| π |
| 12 |
∴直线l与平面A1BD所成角的取值范围是[
| π |
| 12 |
| 5π |
| 12 |
故选:C.
点评:本题考查了二面角的平面角、线面角、三垂线定理、异面直线所成的角,考查了空间想象能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
位于坐标原点的一个支点P按下述规则移动:质点每次移动一个单位:移动的方向为向上或向右,并且向上、向右移动的概率都是0.5,质点P移动6次后位于点(2,4)的概率为( )
A、(
| ||||||
B、C
| ||||||
C、C
| ||||||
D、C
|
定义在R上的函数f(x)满足f(-x)+f(x)且周期是4,若f(1)=5,则f(2015)( )
| A、5 | B、-5 | C、0 | D、3 |
若直线y=k(x+4)与曲线x=
有交点,则k的取值范围是( )
| 4-y2 |
A、[-
| ||||||||
B、(-∞,-
| ||||||||
C、[-
| ||||||||
D、(-∞,-
|