题目内容
设数列{an}满足 ,an+1=an2+an(n∈N*),记
,an+1=an2+an(n∈N*),记 ,则S10的整数部分为
,则S10的整数部分为
- A.1
- B.2
- C.3
- D.4
B
分析:由数列{an}满足 ,an+1=an2+an(n∈N*),知
,an+1=an2+an(n∈N*),知 =
= =
= ,所以
,所以 ,故
,故 +…+
+…+ =
= ,由此能够求出S10的整数部分.
,由此能够求出S10的整数部分.
解答:∵数列{an}满足 ,an+1=an2+an=an(an+1)(n∈N*),
,an+1=an2+an=an(an+1)(n∈N*),
∴ =
= =
= =
= ,
,
∴ ,
,
∴ +…+
+…+ =
= ,
,
∵ ,
,
 ,
,
 ,
,
 +
+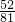 >1,
>1,
又an+1>an,
∴a11>1,
∴0< <1,
<1,
∵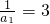 ,
,
∴S10的整数部分是2.
故选B.
点评:本题考查数列的递推式,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.
分析:由数列{an}满足
 ,an+1=an2+an(n∈N*),知
,an+1=an2+an(n∈N*),知 =
= =
= ,所以
,所以 ,故
,故 +…+
+…+ =
= ,由此能够求出S10的整数部分.
,由此能够求出S10的整数部分.解答:∵数列{an}满足
 ,an+1=an2+an=an(an+1)(n∈N*),
,an+1=an2+an=an(an+1)(n∈N*),∴
 =
= =
= =
= ,
,∴
 ,
,∴
 +…+
+…+ =
= ,
,∵
 ,
, ,
, ,
, +
+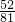 >1,
>1,又an+1>an,
∴a11>1,
∴0<
 <1,
<1,∵
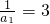 ,
,∴S10的整数部分是2.
故选B.
点评:本题考查数列的递推式,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目