题目内容
设数列满足：a1=1，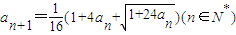
．（1）求a2，a3；
（2）令
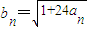，求数列的通项公式．
【答案】分析：（1）利用数列{an}满足：a1=1，
，代入计算，可得a2，a3；
（2）证明{bn-3}是以2为首项，以
为公比的等比数列，即可求数列的通项公式．
解答：解：（1）∵数列{an}满足：a1=1，
，
∴
=
，
=
=
．
（2）∵
，∴
，代入
得
化简可得
，即2bn+1=bn+3．
∴2（bn+1-3）=bn-3，∴{bn-3}是以2为首项，以
为公比的等比数列，
∴bn-3=
，∴bn=
+3．
点评：本题主要考查等比数列的定义和性质，根据递推关系求通项公式，考查学生的计算能力，属于中档题．
，代入计算，可得a2，a3；（2）证明{bn-3}是以2为首项，以
为公比的等比数列，即可求数列的通项公式．解答：解：（1）∵数列{an}满足：a1=1，
，∴
=，==．（2）∵
，∴，代入 得
化简可得
，即2bn+1=bn+3．∴2（bn+1-3）=bn-3，∴{bn-3}是以2为首项，以
为公比的等比数列，∴bn-3=
，∴bn=+3．点评：本题主要考查等比数列的定义和性质，根据递推关系求通项公式，考查学生的计算能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
}满足
=
2-nan+1,n=1,2,3,….?
}满足
=
2-n
+1,n=1,2,3,…,当a1=2时,求a2,a3,a4,并由此猜想an的一个通项公式.
,
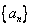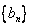满足：a1=4，a2=
,
,
.?
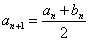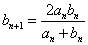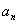表示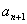
；并证明：对任意
,
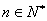an>2 ;?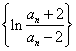 
是等比数列；?
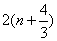是否有确定的大小关系？若有，加以证明；若没有，请说明理由.