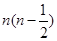题目内容
?
设数列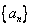 ,
,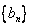 满足:a1=4,a2=
满足:a1=4,a2= ,
,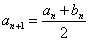 ,
,
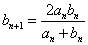 .?
.?
(1)用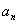 表示
表示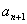 ;并证明:对任意
;并证明:对任意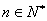 ,
an>2 ;?
,
an>2 ;?
(2)证明: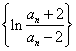 是等比数列;?
是等比数列;?
(3)设Sn是数列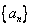 的前n项和,当n≥2时,Sn与
的前n项和,当n≥2时,Sn与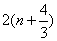 是否有确定的大小关系?若有,加以证明;若没有,请说明理由.
是否有确定的大小关系?若有,加以证明;若没有,请说明理由.
【答案】
解(1)由已知得a1=4,a2= ,所以
,所以 1分?
1分?
故 ;
;
由已知: ,
, ,
, ,
, ∴
∴ ,
,
由均值不等式得 4分
4分
故? ,
, 5分
5分
(2)
 ,
,


得 , 所以
, 所以 是等比数列 8分
是等比数列 8分
(3)由(2)可知 ∴
∴
 当n≥2时,
当n≥2时,  10分?
10分?
∴ ,
,  ,…,
,…,
相加得: 12分?
12分?
∵ ,
, ,?∴
,?∴
∴
故n≥2时, 14分?
14分?

练习册系列答案
相关题目
设数列 满足:
满足:  , 则
, 则 =" " ( )
=" " ( )
A. | B.3 | C. | D. |
 满足
满足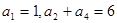 ,且对任意
,且对任意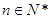 ,函数
,函数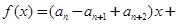
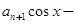
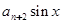 满足
满足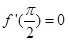 ,若
,若 ,则数列
,则数列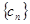 的前
的前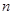 项和
项和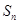 为( )
为( ) B.
B.
 D.
D.
 满足:
满足:  , 则
, 则 = ( )
= ( ) B.3
C.
B.3
C.  D.
D.
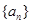 满足
满足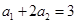 ,且对任意的
,且对任意的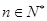 ,点
,点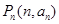 都有
都有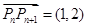 ,则
,则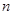 项和
项和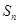 为( )
为( )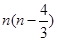 B.
B.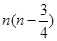 C.
C.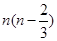 D.
D.