题目内容
14. 已知四边形ABCD是矩形,AB=1,AD=2,E,F分别是线段AB,BC的中点,PA⊥平面ABCD.
已知四边形ABCD是矩形,AB=1,AD=2,E,F分别是线段AB,BC的中点,PA⊥平面ABCD.(1)求证:DF⊥平面PAF;
(2)若∠PBA=45°,求三棱锥C-PFD的体积;
(3)在棱PA上是否存在一点G,使得EG∥平面PFD,若存在,请求出$\frac{AG}{AP}$的值,若不存在,请说明理由.
分析 (1)由勾股定理的逆定理可得DF⊥AF,由PA⊥平面ABCD得PA⊥DF,故而DF⊥平面PAF;
(2)根据PA⊥AB,∠PBA=45°可得PA=1,把△CDF作棱锥的底面,则PA为棱锥的高;
(3)过E作EH∥DF交AD于H,过H作HG∥PD,则平面EGH∥平面PDF,根据长方形的性质和平行线等分线段成比例定理可求得$\frac{AG}{AP}$的值.
解答 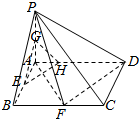 解:(1)在矩形ABCD中,∵F是BC的中点,AB=1,AD=2,
解:(1)在矩形ABCD中,∵F是BC的中点,AB=1,AD=2,
∴AF=DF=$\sqrt{2}$,∴AF2+DF2=4=AD2,
∴DF⊥AF.
∵PA⊥平面ABCD,DF?平面ABCD,
∴PA⊥DF,
又∵PA?平面PAF,AF?平面PAF,PA∩AF=A,
∴DF⊥平面PAF.
(2)∵PA⊥平面ABCD,AB?平面ABCD,
∴PA⊥AB,∵∠PBA=45°,
∴PA=AB=1.
∴三棱锥C-PFD的体积V=$\frac{1}{3}$S△CDF×PA=$\frac{1}{3}×\frac{1}{2}×1×1×1$=$\frac{1}{6}$.
(3)过E作EH∥DF交AD于H,过H作HG∥PD,
则平面EGH∥平面PDF,
∴EG∥平面PDF.
∵EH∥DF,∴$\frac{AH}{AD}=\frac{1}{4}$,
又∵HG∥PD,∴$\frac{AG}{AP}=\frac{AH}{AD}=\frac{1}{4}$.
点评 本题考查了线面垂直的性质与判定,线面平行的判定,棱锥的体积计算,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)与直线y=2x无交点,则离心率e的取值范围是( )
| A. | (1,2) | B. | (1,2] | C. | (1,$\sqrt{5}$) | D. | (1,$\sqrt{5}$] |
9.把三进制数1021(3)化为十进制数等于( )
| A. | 102 | B. | 34 | C. | 12 | D. | 46 |
19.设F1、F2是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左、右焦点,P为直线$x=-\frac{4}{3}a$上一点,△F1PF2是底角为30°的等腰三角形,则此椭圆C的离心率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{8}{9}$ |