题目内容
(本小题满分13分)已知函数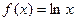
(1)求函数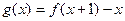 的最大值;
的最大值;
(2)当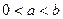 时,求证
时,求证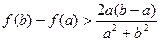 ;
;
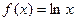
(1)求函数
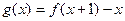 的最大值;
的最大值;(2)当
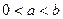 时,求证
时,求证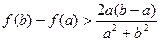 ;
;(1)

 令
令 得
得
当 时,
时, 当
当 时
时 ,又
,又
 当且仅当
当且仅当 时,
时, 取得最大值0 -----------7分
取得最大值0 -----------7分
(2)
由(1)知
又
 -------------13分
-------------13分


 令
令 得
得
当
 时,
时, 当
当 时
时 ,又
,又
 当且仅当
当且仅当 时,
时, 取得最大值0 -----------7分
取得最大值0 -----------7分(2)

由(1)知

又

 -------------13分
-------------13分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
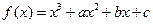 是定义在
是定义在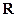 上的奇函数,其图象过点
上的奇函数,其图象过点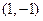 和
和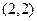 .
.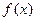 的解析式,并求
的解析式,并求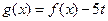 ,当实数
,当实数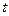 如何取值时,关于
如何取值时,关于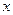 的方程
的方程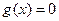 有且只有一个实
有且只有一个实
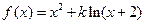 ,其中
,其中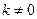
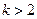 判断
判断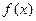 在
在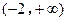 上的单调性.
上的单调性.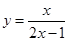 在点(1,1)处的切线方程为( )
在点(1,1)处的切线方程为( )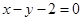
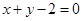
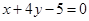
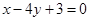
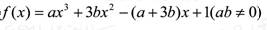 在x=1处取得极值,在x=2处的切线平行于向量
在x=1处取得极值,在x=2处的切线平行于向量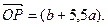
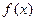 的单调区间;
的单调区间;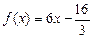 在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.
在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.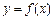 及其导函数
及其导函数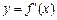 的图象如图所示,则曲线
的图象如图所示,则曲线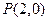 处的切线方程是
处的切线方程是 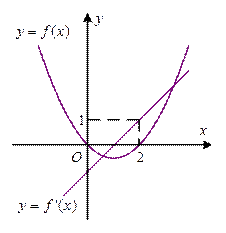
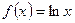 ,若直线
,若直线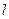 与
与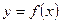 的图象相切的切点的横坐标为1,那么直线
的图象相切的切点的横坐标为1,那么直线
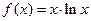 的单调递减区间是 .
的单调递减区间是 .