题目内容
(本小
 题满分14分)设函数
题满分14分)设函数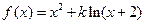 ,其中
,其中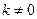
(Ⅰ)当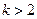 判断
判断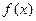 在
在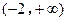 上的单调性.
上的单调性.
(Ⅱ)讨论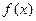 的极值点.
的极值点.

 题满分14分)设函数
题满分14分)设函数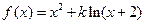 ,其中
,其中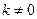
(Ⅰ)当
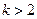 判断
判断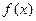 在
在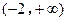 上的单调性.
上的单调性.(Ⅱ)讨论
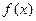 的极值点.
的极值点.解:(理)由题设函数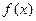 定义域是
定义域是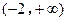 ,…………………1分
,…………………1分
函数 ………………①
………………①
……………… ………………………………2分
………………………………2分
(Ⅰ).当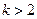 时,①式的
时,①式的 ,
,
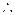
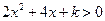 ,又
,又
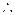
 ………………………………………………4分
………………………………………………4分
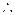
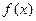 在
在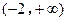 上的单调递增.………………………………………………5分
上的单调递增.………………………………………………5分
(Ⅱ).
(1) 当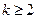 时,由(Ⅰ)知
时,由(Ⅰ)知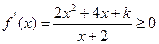 ,
,
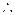
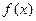 在
在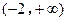 上的单调递增,故
上的单调递增,故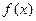 无极值点.……………………………7分
无极值点.……………………………7分
(2) 当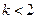 时,由
时,由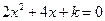 解得
解得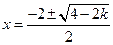 ,此时
,此时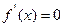
当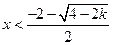 或
或 时,
时,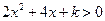
当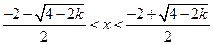 时,
时,
………………………………………………8分
① 当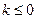 时,
时,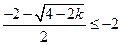 ,
,
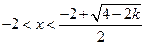 时,
时,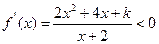 ,
,
 ,
,
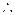
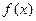 在
在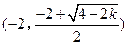 上单减,在
上单减,在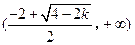 上单增,
上单增,
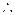
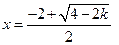 为极小值点,无极大值点.………………………………10分
为极小值点,无极大值点.………………………………10分
② 当 时,
时, ,
,
当 或
或 时,
时,
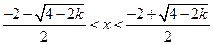 时,
时,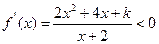
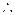
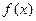 在
在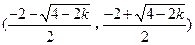 上单减,在
上单减,在 和
和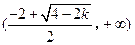 上单增,
上单增,
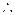
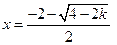 为极大值点,
为极大值点,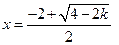 为极小值点.……………12分
为极小值点.……………12分
综上,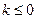 时,
时,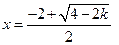 为极小值点,无极大值点;
为极小值点,无极大值点; 时,
时,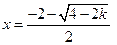 为极大值点,
为极大值点,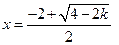 为极小值点;
为极小值点;
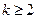 时,
时,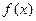 无极值点. ………………………14分
无极值点. ………………………14分
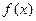 定义域是
定义域是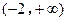 ,…………………1分
,…………………1分函数
 ………………①
………………①………………
 ………………………………2分
………………………………2分(Ⅰ).当
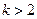 时,①式的
时,①式的 ,
,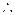
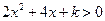 ,又
,又
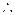
 ………………………………………………4分
………………………………………………4分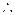
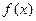 在
在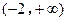 上的单调递增.………………………………………………5分
上的单调递增.………………………………………………5分(Ⅱ).
(1) 当
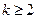 时,由(Ⅰ)知
时,由(Ⅰ)知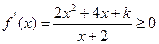 ,
,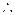
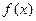 在
在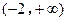 上的单调递增,故
上的单调递增,故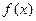 无极值点.……………………………7分
无极值点.……………………………7分(2) 当
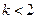 时,由
时,由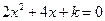 解得
解得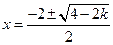 ,此时
,此时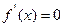
当
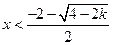 或
或 时,
时,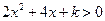
当
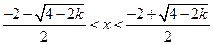 时,
时,
………………………………………………8分
① 当
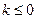 时,
时,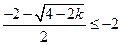 ,
,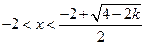 时,
时,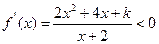 ,
, ,
,
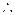
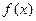 在
在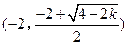 上单减,在
上单减,在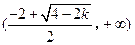 上单增,
上单增,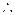
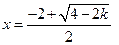 为极小值点,无极大值点.………………………………10分
为极小值点,无极大值点.………………………………10分② 当
 时,
时, ,
,当
 或
或 时,
时,
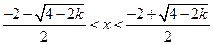 时,
时,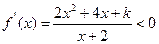
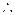
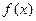 在
在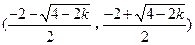 上单减,在
上单减,在 和
和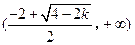 上单增,
上单增,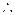
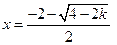 为极大值点,
为极大值点,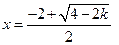 为极小值点.……………12分
为极小值点.……………12分综上,
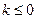 时,
时,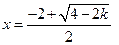 为极小值点,无极大值点;
为极小值点,无极大值点; 时,
时,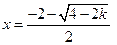 为极大值点,
为极大值点,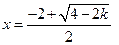 为极小值点;
为极小值点;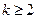 时,
时,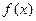 无极值点. ………………………14分
无极值点. ………………………14分略

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
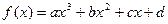 (a、b、c、d∈R)满足:
(a、b、c、d∈R)满足: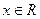 都有
都有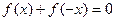 ,
,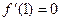 ,
,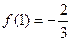
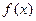 的解析式;
的解析式;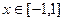 时,证明:函数图象上任意两点处的切线不可能互相垂直;
时,证明:函数图象上任意两点处的切线不可能互相垂直;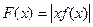 ,证明:
,证明: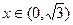 时,
时,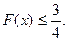
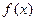 是定义在
是定义在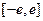 上的奇函数,当
上的奇函数,当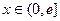 时,
时,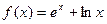 ,其中
,其中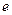 是自然对数的底数.
是自然对数的底数.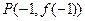 处的切线方程.
处的切线方程. 某厂家拟在2012年举行促销活动,经调查测算,该产品的
某厂家拟在2012年举行促销活动,经调查测算,该产品的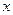 万件与年促销费用
万件与年促销费用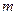 万元(
万元( (
( 为
为 两部分资金).
两部分资金). 润最大?
润最大?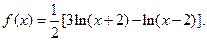
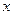 为何值时,
为何值时,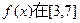 上取得最大值;
上取得最大值;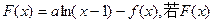 是单调递增函数,求
是单调递增函数,求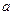 的取值范围.
的取值范围.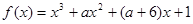 有极大值和极小值,则实数a的取值范围是( )
有极大值和极小值,则实数a的取值范围是( )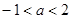
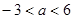
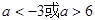
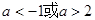
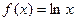
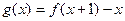 的最大值;
的最大值;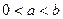 时,求证
时,求证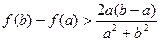 ;
;
 即可,不必算出最结果.)
即可,不必算出最结果.)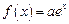 ,
,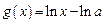 ,其中a为常数,且函数y=f(x)和y=g(x)的图像在其与两坐标轴的交点处的切线相互平行.若关于x的不等式
,其中a为常数,且函数y=f(x)和y=g(x)的图像在其与两坐标轴的交点处的切线相互平行.若关于x的不等式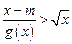 对任意不等于1的正实数都成立,则实数m的取值集合是____________。
对任意不等于1的正实数都成立,则实数m的取值集合是____________。