题目内容
已知曲线y=x -
在点(1,1)处的切线为直线l,则l与两坐标轴所围成的三角形面积为 .
| 1 |
| 2 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:求出函数的导数,求得在点(1,1)处的切线斜率,再由点斜式方程可得切线方程,再分别令x=0,y=0,再由三角形的面积公式,即可得到.
解答:
解:求导数可得y′=-
•x-
,
所以在点(1,1)处的切线斜率为-
,
切线方程为:y-1=-
(x-1),
令x=0,得y=
;令y=0,得x=3.
所以切线与两坐标轴围成的三角形的面积为
×
×3=
,
故答案为:
.
| 1 |
| 2 |
| 3 |
| 2 |
所以在点(1,1)处的切线斜率为-
| 1 |
| 2 |
切线方程为:y-1=-
| 1 |
| 2 |
令x=0,得y=
| 3 |
| 2 |
所以切线与两坐标轴围成的三角形的面积为
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
故答案为:
| 9 |
| 4 |
点评:本题考查导数的几何意义,考查学生的计算能力,确定切线方程是关键.

练习册系列答案
相关题目
设A={x|2014≤x≤2015},B={x|x<a},若A⊆B,则实数a的取值范围是( )
| A、a>2014 |
| B、a>2015 |
| C、a≥2014 |
| D、a≥2015 |
已知全集U={1,2,3},且2∉A,则集合A的子集最多有 ( )
| A、4个 | B、5个 | C、6个 | D、7个 |
下列关系式正确的是( )
A、
| ||
| B、{2}={x|x2=2x} | ||
| C、{a,b}={b,a} | ||
| D、Φ∈{2006} |
执行如图所示的程序框图,如果输入的x,y,N的值分别为1,2,3,则输出的S=( )
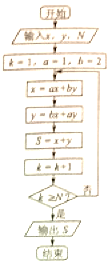

| A、27 | B、81 | C、99 | D、577 |
有一家三口的年龄之和为65岁,设父亲、母亲和小孩的年龄分别为x、y、z,则下列选项中能反映x、y、z关系的是( )
| A、x+y+z=65 | |||||||
B、
| |||||||
C、
| |||||||
D、
|
已知数列{an}的前n项和Sn=n2-6n,数列{|an|}的前n项和Tn,则
的最小值是( )
| Tn |
| n |
A、6
| ||
B、
| ||
C、
| ||
| D、3 |