题目内容
已知函数 (
( ).
).
(Ⅰ)若 的定义域和值域均是
的定义域和值域均是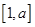 ,求实数
,求实数 的值;
的值;
(Ⅱ)若 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的 ,
,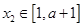 ,总有
,总有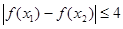 ,求实数
,求实数 的取值范围.
的取值范围.
(Ⅰ)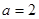 ;(Ⅱ)
;(Ⅱ)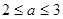 ,
,
解析试题分析:(Ⅰ)利用二次函数在区间上的单调性求解;(Ⅱ)分析二次函数在区间上的单调性,然后把恒成立问题转化最值.
试题解析:(Ⅰ) ∵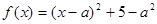 (
(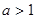 ),
),
∴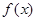 在
在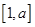 上是减函数
上是减函数
又定义域和值域均为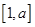 ,
,
∴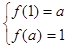 , 即
, 即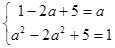 ,解得
,解得 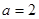 .
.
(II) ∵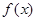 在区间
在区间 上是减函数,∴
上是减函数,∴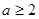 ,
,
又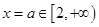 ,且
,且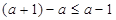
∴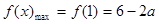 ,
,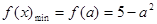 .
.
∵对任意的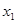 ,
,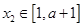 ,总有
,总有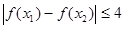 ,
,
∴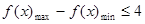 ,即
,即 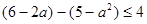 ,解得
,解得  ,
,
又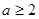 , ∴
, ∴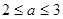 .
.
考点:二次函数的单调性,考查学生的分析计算能力.

练习册系列答案
相关题目
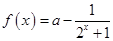 .
. 为何实数,
为何实数, 总是增函数;
总是增函数;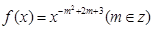 为偶函数,且在区间
为偶函数,且在区间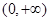 上是单调增函数
上是单调增函数 的解析式;
的解析式;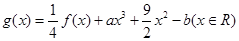 ,其中
,其中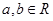 .若函数
.若函数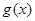 仅在
仅在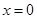 处有极值,求
处有极值,求 的取值范围.
的取值范围.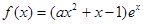 ,其中
,其中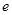 是自然对数的底数,
是自然对数的底数,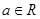 .
.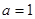 ,求曲线
,求曲线 在点
在点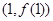 处的切线方程;
处的切线方程;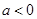 ,求
,求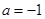 ,函数
,函数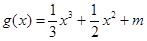 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数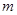 的取值范围.
的取值范围. 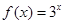 ,
,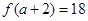 ,
,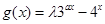 的定义域为
的定义域为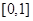
 的值;
的值;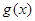 在区间
在区间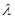 的取值范围。
的取值范围。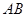 长为2m,跳水板距水面
长为2m,跳水板距水面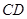 的高
的高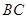 为3m,
为3m, =5m,
=5m,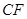 =6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点
=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点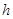 m(
m(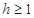 )时达到距水面最大高度4m,规定:以
)时达到距水面最大高度4m,规定:以 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.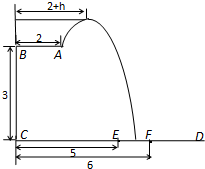
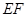 内入水时才能达到压水花的训练要求,求达到压水花的训练要求时
内入水时才能达到压水花的训练要求,求达到压水花的训练要求时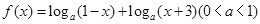 .
. 的定义域 ;
的定义域 ;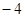 ,求实数
,求实数 的值.
的值. .设某商品标价为
.设某商品标价为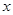 元,购买该商品得到的实际折扣率为
元,购买该商品得到的实际折扣率为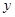 .
. 时,
时,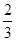 ?
?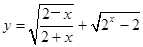 的定义域为
的定义域为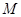 ,
, 时,求函数
时,求函数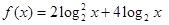 的最大值。
的最大值。