题目内容
已知函数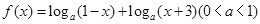 .
.
(1)求函数 的定义域 ;
的定义域 ;
(2)若函数 的最小值为
的最小值为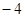 ,求实数
,求实数 的值.
的值.
(1) ;(2)
;(2)
解析试题分析:(1)函数的定义域是使函数解析式有意义的自变量的取值范围,由对数函数的性质得 ,解出
,解出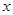 ,写成集合的形式就是函数的定义域;(2)将函数化简得,
,写成集合的形式就是函数的定义域;(2)将函数化简得, ,由
,由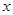 的取值范围得,
的取值范围得, ,解得
,解得 的值为
的值为
试题解析:(1)要使函数有意义:则有 ,解之得
,解之得 . 3分
. 3分
所以函数的定义域为 4分
4分
(2)函数可化为 . 6分
. 6分 ,
, . 8分
. 8分 ,
, ,即
,即 . 9分
. 9分
由 ,得
,得 ,
, . 11分
. 11分
故实数 的值为
的值为 12分
12分
考点:1.对数式的运算性质;2.对数函数单调性;3.不等式.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
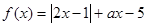 (a是常数,a∈R)
(a是常数,a∈R)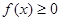 的解集;
的解集;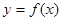 恰有两个不同的零点,求a的取值范围.
恰有两个不同的零点,求a的取值范围. (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式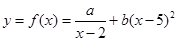 ,其中
,其中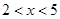 ,
, 为常数,已知销售价格为4元/千克时,每日可销售出该商品5千克;销售价格为4.5元/千克时,每日可销售出该商品2.35千克.
为常数,已知销售价格为4元/千克时,每日可销售出该商品5千克;销售价格为4.5元/千克时,每日可销售出该商品2.35千克. 的解析式;
的解析式; (
( ).
). 的定义域和值域均是
的定义域和值域均是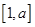 ,求实数
,求实数 的值;
的值; 上是减函数,且对任意的
上是减函数,且对任意的 ,
,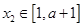 ,总有
,总有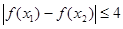 ,求实数
,求实数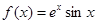 .
.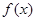 的单调区间;
的单调区间;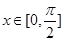 ,
,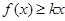 总成立,求实数
总成立,求实数 的取值范围;
的取值范围;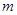 ,使得:当
,使得:当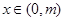 时,不等式
时,不等式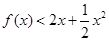 恒成立?请给出结论并说明理由.
恒成立?请给出结论并说明理由. 为偶函数,且在区间
为偶函数,且在区间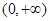 上是单调增函数.
上是单调增函数. 的解析式;
的解析式; ,若
,若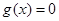 的两个实根分别在区间
的两个实根分别在区间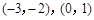 内,求实数
内,求实数 的取值范围.
的取值范围. x2-x+
x2-x+ 是[1,b]上的“四维光军”函数,求常数b的值;
是[1,b]上的“四维光军”函数,求常数b的值;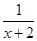 是区间[a,b]上的“四维光军”函数?若存在,求出a,b的值,否则,请说明理由.
是区间[a,b]上的“四维光军”函数?若存在,求出a,b的值,否则,请说明理由. 的等边三角形
的等边三角形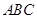 的顶点
的顶点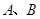 处(如图),现要在边
处(如图),现要在边 上的
上的 点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返
点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返 车间5次,往返
车间5次,往返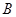 车间20次,设叉车每天往返的总路程为
车间20次,设叉车每天往返的总路程为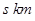 .(注:往返一次即先从仓库到车间再由车间返回仓库)
.(注:往返一次即先从仓库到车间再由车间返回仓库)
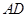 长为
长为 ,将
,将 表示成
表示成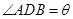 ,将
,将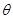 的函数关系式.
的函数关系式.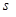 的最小值,并指出点
的最小值,并指出点 是定义在
是定义在 上的偶函数,且
上的偶函数,且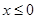 时,
时, .
. 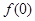 ,
,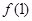 ;
;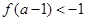 ,求
,求 的取值范围.
的取值范围.