题目内容
已知函数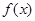 满足对任意的
满足对任意的 恒有
恒有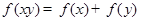 ,且当
,且当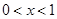 时,
时,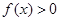 .
.
(1)求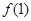 的值;
的值;
(2)判断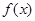 的单调性
的单调性
(3)若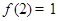 ,解不等式
,解不等式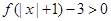 .
.
(1)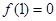 ;(2)
;(2)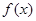 在
在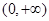 单调递减;(3)
单调递减;(3)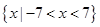 .
.
解析试题分析:(1)采用附值:将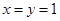 代入
代入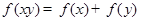 即可出
即可出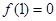 ;(2)由题中条件
;(2)由题中条件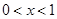 时,
时,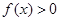 ,先设
,先设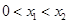 ,进而得到
,进而得到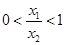 ,由函数单调性的定义,转为判断
,由函数单调性的定义,转为判断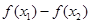 的符号即可,而
的符号即可,而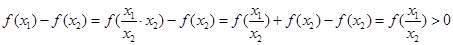 ,进而可得
,进而可得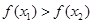 ,这样即可得到
,这样即可得到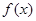 在
在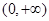 的单调性;(3)先由
的单调性;(3)先由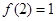 推出
推出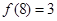 ,进而结合(2)中函数
,进而结合(2)中函数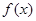 的单调性,可将不等式
的单调性,可将不等式 ,进而求解不等式即可.
,进而求解不等式即可.
(1)令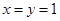 ,可得
,可得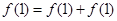 ,即
,即
故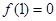 3分
3分
(2)任取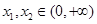 ,且
,且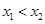 ,则
,则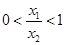
由于当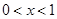 时,
时,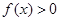 ,∴
,∴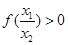 5分
5分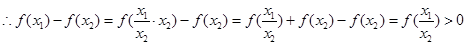
∴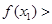
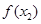
∴函数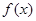 在
在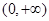 上是单调递减函数 8分
上是单调递减函数 8分
(3)由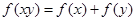 得
得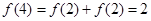
∴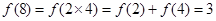 10分
10分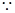 函数
函数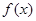 在区间
在区间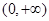 上是单调递减函数
上是单调递减函数
∴不等式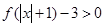
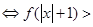
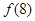
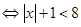
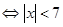
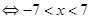
∴不等式的解集为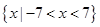 14分.
14分.
考点:1.抽象函数;2.函数的单调性的证明;3.函数的单调性在求解不等式的应用;4.绝对值不等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是
是 上的奇函数,且当
上的奇函数,且当 时,
时, .
.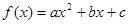 (a≠0)满足
(a≠0)满足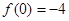 ,
,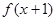 为偶函数,且x=-2是函数
为偶函数,且x=-2是函数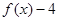 的一个零点.又
的一个零点.又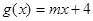 (
( >0).
>0).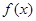 的解析式;
的解析式;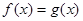 在
在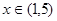 上有解,求实数
上有解,求实数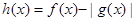 ,求
,求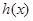 的单调区间.
的单调区间.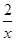 且f(4)=
且f(4)=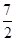 .
.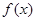 定义在
定义在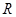 上,对任意的
上,对任意的 ,
,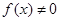 ,且
,且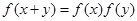 .
.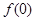 ,并证明:
,并证明: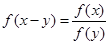 ;
;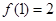 .设向量
.设向量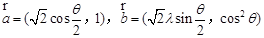 ,对任意
,对任意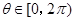 ,
, 恒成立,求实数
恒成立,求实数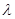 的取值范围.
的取值范围.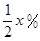 ,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
,该产品每吨的价格上涨百分之几,可使销售的总金额最大?