题目内容
函数y=sinx的图象向左平移φ(0≤φ<2π)个单位后得到函数y=sin(x-
)的图象,则φ等于( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:命题的真假判断与应用
专题:计算题,三角函数的图像与性质
分析:先根据图象变换得到平移后的函数y=sin(x+φ),然后结合诱导公式可得到sin(x+
π)=sin(x-
),进而可确定答案.
| 5π |
| 3 |
| π |
| 3 |
解答:
解:将函数y=sinx的图象向左平移φ(0≤φ<2π)个单位
得到函数y=sin(x+φ)的图象.
根据诱导公式知,
当φ=
时,有y=sin(x+
)=sin(x+2π-
)
=sin(x-
).
故选D.
得到函数y=sin(x+φ)的图象.
根据诱导公式知,
当φ=
| 5π |
| 3 |
| 5π |
| 3 |
| π |
| 3 |
=sin(x-
| π |
| 3 |
故选D.
点评:本题主要考查图象变换和诱导公式的应用.考查对基础知识的综合运用.

练习册系列答案
相关题目
定义在R上的函数f(x)=sinx+2xf′(
),f′(x)为f(x)的导函数,令a=-
,b=log32,则下列关系正确的是( )
| π |
| 3 |
| 1 |
| 2 |
| A、f(a)+f(b)<0 |
| B、f(-a)+f(b)>0 |
| C、f(a)+f(-b)<0 |
| D、f(-a)+f(-b)<0 |
直线y=kx+k与椭圆
+
=1的位置关系是( )
| x2 |
| 3 |
| y2 |
| 2 |
| A、相交 | B、相切 | C、相离 | D、不确定 |
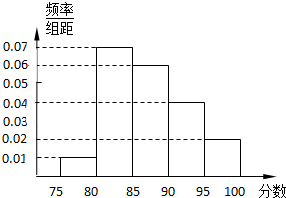 某高中进行高中生歌唱比赛,在所有参赛成绩中随机抽取100名学生的成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试.
某高中进行高中生歌唱比赛,在所有参赛成绩中随机抽取100名学生的成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试.