题目内容
已知直线a，b和平面α，其中a?α，b?α，则“a∥b”是“a∥α”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据充分条件和必要条件的定义，线面平行的性质和判定，即可得到结论．
解答：
解：根据线面平行的判定定理可得若a∥b，则a∥α，即充分性成立，
若a∥α，则a∥b不一定成立，故必要性不成立．
故“a∥b”是“a∥α”的充分不必要条件，
故选：A．
若a∥α，则a∥b不一定成立，故必要性不成立．
故“a∥b”是“a∥α”的充分不必要条件，
故选：A．
点评：本题主要考查充分条件和必要条件的应用，利用线面平行的判定定理和性质是解决本题的关键．
练习册系列答案
相关题目
斜三角形ABC中，命题甲：A=
，命题乙：cosB≠
，则甲是乙的（ ）
| π |
| 6 |
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设x，y满足
，则z=x-y（ ）
|
| A、有最小值2，无最大值 |
| B、有最小值-1，无最大值 |
| C、有最大值2，无最小值 |
| D、既无最小值，又无最大值 |
设全集U=R，集合A={x|0≤x≤2}，B={y|1≤y≤3}，则（∁UA）∩B=（ ）
| A、（2，3] |
| B、（-∞，1]∪（2，+∞） |
| C、[1，2） |
| D、（-∞，0）∪[1，+∞） |
在△ABC中，AC=
，AB=3，BC=2，M，N，P分别为AC，AB，BC中点，将△ABC沿MN，NP，MP折起得到三棱锥S-MNP，三棱锥S-MNP外接球的表面积为（ ）
| 7 |
| A、10π | ||
| B、8π | ||
| C、5π | ||
D、
|
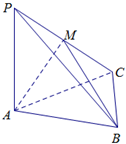如图，底面是正三角形的三棱锥P-ABC中，PA⊥底面ABC，M为PC中点，且PA=AB，其中下列四个命题：在区间[0，π]内随机取两个数分别记为a、b，则使得函数f（x）=x2+2ax-b2+π有零点的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|