题目内容
【题目】已知定义在![]() 上的函数
上的函数![]() ,
,![]() 为其导数,且
为其导数,且![]() 恒成立,则( )
恒成立,则( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
通过![]() ,可以联想到导数运算的除法,这样可以构造新函数
,可以联想到导数运算的除法,这样可以构造新函数
![]() ,
,![]() ,这样就可以判断出函数
,这样就可以判断出函数![]() 在
在![]() 上的单调性,把四个选项变形,利用单调性判断出是否正确.
上的单调性,把四个选项变形,利用单调性判断出是否正确.
通过![]() ,这个结构形式,可以构造新函数
,这个结构形式,可以构造新函数![]() ,
,
![]() ,而
,而![]() ,所以当
,所以当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上是单调递增函数,现对四个选项逐一判断:
上是单调递增函数,现对四个选项逐一判断:
选项A. ![]() ,可以判断
,可以判断![]() 是否正确,
是否正确,
也就是判断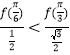 是否正确,即判断
是否正确,即判断![]() 是否成立,因为
是否成立,因为![]() ,
,![]() 在
在![]() 上是单调递增函数,所以有
上是单调递增函数,所以有![]() ,故选项A正确;
,故选项A正确;
选项B.![]() ,也就是判断
,也就是判断![]() 是否正确,即判断
是否正确,即判断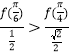 是否成立,即判断
是否成立,即判断![]() 是否成立,因为
是否成立,因为![]() ,
,![]() 在
在![]() 上是单调递增函数,所以有
上是单调递增函数,所以有![]() ,故选项B不正确;
,故选项B不正确;
选项C. ![]() ,也就是判断
,也就是判断![]() 是否正确,即判断
是否正确,即判断
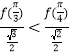 是否成立,即判断
是否成立,即判断![]() 是否成立,因为
是否成立,因为![]() ,
,![]() 在
在![]() 上是单调递增函数,所以有
上是单调递增函数,所以有![]() ,故选项C不正确;
,故选项C不正确;
选项D.![]() ,也就是判断
,也就是判断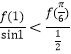 ,是否成立,即判断
,是否成立,即判断![]() 是否成立,因为
是否成立,因为![]() ,
,![]() 在
在![]() 上是单调递增函数,所以有
上是单调递增函数,所以有![]() ,因此选项D不正确,故本题选A.
,因此选项D不正确,故本题选A.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
【题目】某地植被面积 ![]() (公顷)与当地气温下降的度数
(公顷)与当地气温下降的度数![]() (
(![]() )之间有如下的对应数据:
)之间有如下的对应数据:
| 20 | 40 | 50 | 60 | 80 |
| 3 | 4 | 4 | 4 | 5 |
(1)请用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中所求线性回归方程,如果植被面积为200公顷,那么下降的气温大约是多少![]() ?
?
参考公式:用最小二乘法求线性回归方程系数公式: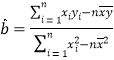 ,
,![]() .
.